Decimal Representation of Irrational Numbers
Decimal expansion of irrational numbers results in non-terminating and non-recurring decimal number. A decimal is a set of numbers that are written together with a decimal point in between them. The numbers to the left of the decimal point are the integers or whole numbers and the numbers to the right of the decimal point are decimal numbers. Let us learn the decimal representation of irrational numbers and solve a few examples to understand the concept better.
| 1. | Decimal Representation of a Number |
| 2. | Decimal Representation of Irrational Number |
| 3. | FAQs on Decimal Expansion of Irrational Numbers |
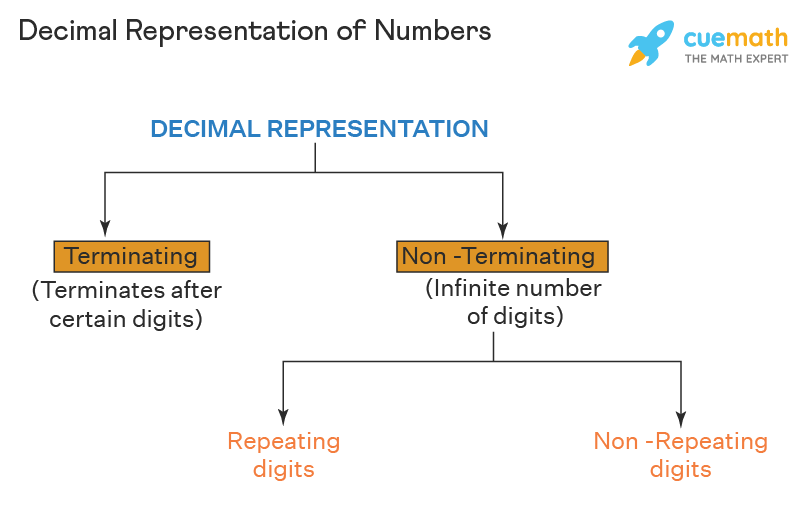
Decimal Representation of a Number
Decimal representation is merely showing any given number in the form of decimal numbers. It will depend upon whether the digits are repeating, non-repeating, end, or un-ending (infinite digits after the decimal point). Let us have a look at how the decimals are categorized based on their type here.
- Terminating decimals: Terminating decimals mean it does not reoccur and end after a finite number of decimal places. For example: 543.534234, 27.2, etc.
- Non-terminating decimals: It means that the decimal numbers have infinite digits after the decimal point. For example, 54543.23774632439473747..., 827.79734394723... etc. The Non-Terminating decimal numbers can be further be divided into 2 parts:
- Recurring decimal numbers: In Recurring Decimal Numbers, digits repeat after a fixed interval. For example, 94346.374374374..., 573.636363... etc,
- Non- recurring decimal numbers: Non- Recurring Decimal Numbers, digit never repeat after a fixed interval. For example 743.872367346.., 7043927.78687564... and so on.
Irrational Numbers
Irrational numbers are real numbers that cannot be simplified into fractions. Thus, the conversion of decimals to fractions for such numbers is also not possible. For example, π (pi) is an irrational number where, π = 3⋅14159265… The decimal value never stops at any point. Since the value of π is closer to the fraction 22/7, we take the value of pi as 22/7 or 3.14.
Decimal Representation of Irrational Number
The decimal representation of irrational numbers means expressing the most accurate value of the irrational number in the form of decimal numbers. Irrational numbers are represented as non-terminating decimals with non-repeating digits. Non-terminating, Non-repeating decimal expansion means that although the decimal representation has an infinite number of digits, there is no pattern to it. The ellipsis or the three dots at the end of each representation, tells us that the sequence of digits never ends and evaluation of these numbers can exist to more and more decimal digits with no end. For example: Let’s think of \(\sqrt 2 \) for a moment. If we try to write \(\sqrt 2 \) in decimal form (say, to 5 decimal digits), we have \(\sqrt 2 = 1.41421 \ldots \). If we expand \(\sqrt 2 \) to 10 decimal digits, it would be \[\sqrt 2 = 1.4142135623\ldots \]
To show the actual value we can represent \(\sqrt 2 \) geometrically. If we construct a right-angled triangle with the two sides each of length 1 unit, the hypotenuse is exactly \(\sqrt 2 \) units. Thus, we see that even though the decimal representation might be less than exact (no matter how many digits you take in your decimal representation), the geometrical representation is exact.
Related Topics
Listed below are a few topics related to the decimal expansion of irrational numbers, take a look.
FAQs on Decimal Expansion of Irrational Numbers
How Do You Express an Irrational Number as a Decimal?
An irrational number cant be expressed in the form of a ratio or in the form of a fraction since there is no finite number when written as a decimal. Instead, the numbers in the decimal form would go on forever i.e. will be non-terminating decimals with non-repeating digits.
What are the Decimal Expansion of Irrational and Rational Numbers?
Any decimal number whose terms are terminating or non-terminating but repeating is a rational number. Whereas if the terms are non-terminating and non-repeating, is an irrational number.
How Does Decimal Representation of Irrational Number Look Like?
Irrational numbers in a decimal expansion form result in non-terminating and non-repeating numbers. For example, π is an irrational number and is expressed as 3.14159. Here, there is no finite number of digits that can represent the exact value nor the number repeats.
Are all Irrational Numbers Terminating?
Irrational numbers have non-terminating, non-recurring decimals. Thus no irrational number has a terminating decimal.
Is the Square Root of 3 a Non-Terminating Decimal?
Ans. Yes, all square roots which aren't integers, are irrational numbers. Thus square root of 3 is a non-terminating decimal.
Is 0.333 Recurring an Irrational Number?
No, it is a rational number, as it is a non-terminating, repeating decimal number.
Is 0.7 an Irrational Number?
No, it is a rational number since it is a terminating decimal.