Recurring Decimal
Recurring Decimal, also called as repeating decimal, is a decimal number only that consists of digits repeating after a fixed interval after the decimal. For example, 46.374374374..., 5173.838383... etc. Decimals can be classified into different categories depending upon what type of digits occur after the decimal point, whether the digits are repeating, non-repeating, end, or unending (infinite digits after the decimal point).
In this lesson, let's learn about recurring decimals, recurring decimals as rational numbers, and recurring decimal to fraction with solved examples.
| 1. | What is Recurring Decimal? |
| 2. | Recurring Decimals as Rational Numbers |
| 3. | Recurring Decimal to Fraction |
| 4. | Recurring Decimal Examples |
| 5. | FAQs on Recurring Decimal |
What is Recurring Decimal?
Recurring or repeating decimals are the ones, which have a fixed set of terms after the right of the decimal to be repeated uniformly. The classification of decimal numbers includes terminating and non-terminating decimals, repeating and non-repeating decimals.
Recurring Decimal Definition
A decimal in which to the right of the decimal, a particular digit or sequence of digits repeats itself indefinitely is called as recurring or repeating decimals. It refers to the decimal representation of a number whose digits are periodic (repeating its values at regular intervals) and the infinitely repeated portion is not zero.
Recurring Decimal Representation
A recurring decimal is a non-terminating decimal that has a digit or a sequence of digits repeating over and over and over again without ever ending.
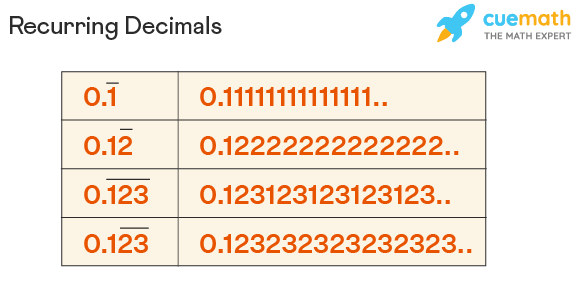
- Mostly, bars are used over the repeating digits in the recurring decimals, for example, 0.333333…..=0.3¯, the repeated term in decimal is represented by a bar on top of the repeated part.
- Dot notation is used with recurring decimals. The dot over the particular digit or digits show which digit is repeating itself, for example, \(0.5 \dot{7}\) is equal to 0.5777777... and \(0. \dot{2} \dot{7}\) is equal to 0.27272727...
Recurring Decimals as Rational Numbers
A rational number can be represented as a decimal number that has the same mathematical value, with the help of the long division method. We need to divide the given rational number using the long division method and the quotient which we get is the decimal representation of that rational number. A rational number can have two types of decimal representations (expansions):
- Terminating
- Non-terminating but repeating
For example, 5/6 = 0.833333... is a recurring, non-terminating decimal. The digit of 3 is repeating over and over at the end of the decimal. Put a bar above the first digit of 3 to indicate that it repeats. Thus, 5/6 = 0.83bar.

Similarly, 1/3 = 0.33333... is a recurring, non-terminating decimal. The digit 3 in the quotient keeps repeating. Thus, 1/3 = 0.3bar.
Recurring Decimal to Fraction
A decimal number can be expressed in different types and forms, one of them being a recurring decimal. Recurring decimals are numbers in which decimal digits are recurring or repeating. Given below are the steps to convert recurring decimal to fraction.
- Step 1: Let x be the recurring or repeating decimal in expanded form.
- Step 2: Count the number of recurring digits. Let them be n.
- Step 3: Multiply the recurring decimal by 10n.
- Step 4: Subtract the result of step 1 from the result of step 3 to eliminate the recurring part.
- Step 5: Solve for x, express answer as a fraction in its simplest form.
For example, if x = 0.23232323, then the number of recurring digits are two, so multiply with 10 to power 2 = 100. 100x = 23.23232323 , subtracting the two equations we get 99x = 23 or x = 23/99.
Related Topics
Recurring Decimal Examples
-
Example 1: Convert the recurring decimal 0.125125125… to its fractional form.
Solution:
The decimal 0.125125125….. can be written as 0.125¯¯¯¯¯¯¯¯.
Here, 125 consists of three terms, and it is repeated in a continuous manner. Thus, the number of times 9 to be repeated in the denominator becomes three.
0.125¯¯¯¯¯¯¯¯=125/999.
Answer: 0.125125125….. in fractional form is 125/999.
-
Example 2: Determine if 11/25 is a terminating or a non-terminating number.
Solution:
A rational number is terminating if it can be expressed in the form:
p/(2n×5m)
The prime factorization of 25 is 5×5
11/25=11/(20×52)
Answer: 11/25 is a terminating rational number.

FAQs on Recurring Decimal
What Are Recurring and Non-recurring Decimals?
Recurring decimals, also known as repeating decimals, are those decimal numbers that keep on repeating the same value after the decimal point, whereas non-recurring decimal numbers are those which do not repeat their values after the decimal point.
How Do You Show a Decimal is Recurring?
A decimal number is considered recurring if a digit (or group of digits) repeats forever after the decimal point. The part that repeats can be shown either by placing dots over the first and last digits of the repeating pattern or by a bar over the pattern.
What Is a Recurring Decimal Called?
A recurring decimal, as the name suggests is called a repeating decimal, as its decimal representation eventually becomes periodic. In other words, the same sequence of digits to the right of decimal repeats indefinitely.
What Is the Difference Between Recurring and Terminating Decimals?
Terminating decimals end up giving remainder 0, whereas the recurring decimals correspond to repeating decimals as the remainder tends to repeat after some point.
What Do You Mean By a Non-Terminating Recurring Decimal?
Decimals are considered non-terminating repeating decimals or recurring decimals if a digit or a sequence of digits in the decimal part keeps repeating itself infinitely. However, the repeating decimal can be expressed by putting a bar over the digit or digits which are repeating themselves.
How Do You Express Recurring Decimals As Rational Numbers?
A rational number can be represented as a decimal number having the same mathematical value, with the help of the long division method. Just divide the given rational number using the long division method and the quotient so obtained is the decimal representation of that rational number. For example, 1/3 (rational number) can be expressed as 0.33333 (recurring, non-terminating decimal). The digit 3 in the quotient keeps repeating. Thus, 1/3 = 0.3bar.
visual curriculum