1/4 As A Decimal
Four friends, Rocky, Rooney, David, and Sam divided a donut equally among themselves. Sam asked, "What portion of the donut do I have?" Rocky replied, " One fourth." Sam asked again, "Is it possible to write it in a form that has denominator 1?".
Let us help Sam resolve his query in mere few minutes.
This section focuses on representing \( \frac{1}{4} \) as a decimal along with some interactive examples and questions on the representation of \( \frac{3}{8} \) as a decimal, \( \frac{2}{3} \) as a decimal, and decimal to fraction conversion. Do not forget to try practice questions at the end of the page for a quick fun revision.
Lesson Plan
What is 1/4 as a Decimal?
When we convert a fraction into decimal form, we convert it into a number that has denominator 1. So the numerator takes a form that has a decimal in it.
The decimal form of \(\dfrac{1}{4}\,\) is 0.25
Let's see how to get that.
How to change ¼ as a decimal
The fraction \(\dfrac{1}{4}\,\)can be converted to a form with denomiator 1 by finding its decimal form.
To get the decimal form of \(\dfrac{1}{4}\,\), different methods can be used.
Method 1
In this method, we use long division.
Here, Numerator = 1 and Denominator = 4. Let's divide 1 by 4

So,
\(\dfrac{1}{4}=0.25.....\text{Decimal form}\)
We can use this method for converting any fraction to decimal form.
Method 2
The other method is to convert the fraction into its equivalent fraction with denominator as a power of 10
The first power of 10 is 10 which is not a multiple of 4. So, let's look at the second multiple, 100, which is a multiple of 4
In the fraction \(\dfrac{1}{4}\), denominator = 4

\begin{align} \dfrac{1}{4}&=\dfrac{1\times 25}{4\times 25}\\&=\dfrac{25}{100}\end{align}
Now, observe that there are 2 zeros in the denominator.
So, there will be two digits after decimal in the numerator.
\(\dfrac{1}{4}=0.25\)
Similarly, if we have the fraction \(\dfrac{3}{8}\), we can convert it into decimal by converting it into its equivalent fraction with denominator 1000
\begin{align} \dfrac{3}{8}&=\dfrac{3\times 125}{8\times 125}\\&=\dfrac{375}{1000}\\&=0.375\end{align}
We can even convert a decimal to fraction. For this, we consider the number of digits after the decimal.
Example: Take 0.65. There are two digits after the decimal.
\begin{align} 0.65&= \dfrac{65}{100}\\&=\dfrac{13}{20}\end{align}

- Decimals are used to represent fractions which have value less than 1
- Visualization of 0.25 on a number line:

Solved Examples
| Example 1 |
Harry is struggling to express \(\dfrac{2}{3}\,\) as decimal. Can you help him by using long division method to convert a fraction to decimal?
Solution
As denominator is 3, which is not a factor of 100, we will convert \(\dfrac{2}{3}\,\) as a decimal by long division.

The quotient is 0.6666.....= \(0.\overline{6}\cdot\cdot \)Digit 6 is recurring here as the remainder is going on repeating.
So, we round off 0.6666..... to 0.67 (rounding off upto 2 decimal places).
| \(\therefore\dfrac{2}{3}=0.67\) |
| Example 2 |
Mia wants to express \(\dfrac{3}{8}\,\) as a decimal number using long division. Help her to reach the correct answer.
Solution
Mia needs to divide 3 by 8 and continue dividing till she gets the remainder 0
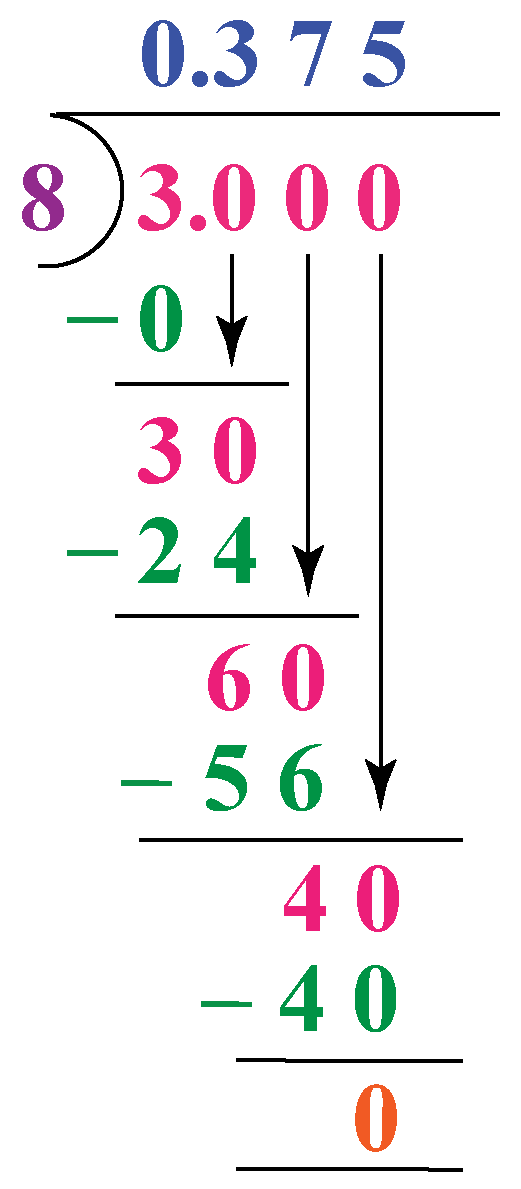
| \(\therefore\)Decimal form of \(\dfrac{3}{8}\) is 0.375 |

Find decimal form of fractions \(\dfrac{1}{5}\) and \(\dfrac{1}{7}\). What difference did you notice in their decimal forms?
(Hint: Observe the remainders in both the cases.)
Interactive Questions
Here are a few activities for you to practice.
Select/Type your answer and click the "Check Answer" button to see the result.
Let's Summarize
We hope you enjoyed learning about 1/4 As A Decimal with the simulations and practice questions. Now, you will be able to easily solve problems on 3/8 as a decimal, 2/3 as a decimal, and decimal to fraction.
About Cuemath
At Cuemath, our team of math experts is dedicated to making learning fun for our favorite readers, the students!
Through an interactive and engaging learning-teaching-learning approach, the teachers explore all angles of a topic.
Be it worksheets, online classes, doubt sessions, or any other form of relation, it’s the logical thinking and smart learning approach that we, at Cuemath, believe in.
Frequently Asked Questions (FAQs)
1. What is \(\dfrac{1}{8}\) as a decimal?
The decimal form of \(\dfrac{1}{8}=0.125\)
2. What is \(\dfrac{9}{20}\) as a decimal?
The decimal form of\(\,\dfrac{9}{20}=0.45\)
3. How do you write \(\dfrac{1}{3}\) as a decimal?
\(\dfrac{1}{3}\) can be written in decimal form as 0.333333....(never ending), which can be rounded off to 0.3
- Live one on one classroom and doubt clearing
- Practice worksheets in and after class for conceptual clarity
- Personalized curriculum to keep up with school