Magnitude and Argument

Consider the complex number \(z = 3 + 4i\). Let us find the distance of z from the origin:

Clearly, using the Pythagoras Theorem, the distance of z from the origin is \(\sqrt {{3^2} + {4^2}}  = 5\) units. Also, the angle which the line joining z to the origin makes with the positive Real direction is \({\tan ^{ - 1}}\left( {\frac{4}{3}} \right)\).

Similarly, for an arbitrary complex number \(z = x + yi\), we can define these two parameters:

1. Modulus of z. This is the distance of z from the origin, and is denoted by \(\left| z \right|\).
2. Argument of z. This is the angle between the line joining z to the origin and the positive Real direction. It is denoted by \(\arg \left( z \right)\).

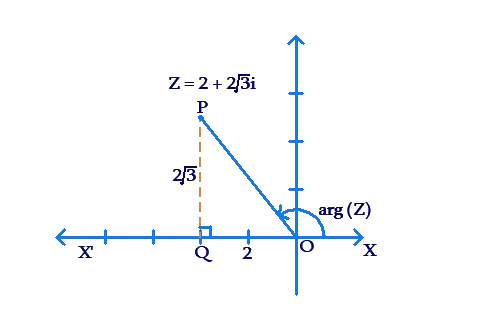
Let us discuss another example. Consider the complex number \(z =  - 2 + 2\sqrt 3 i\), and determine its magnitude and argument. We note that z lies in the second quadrant, as shown below:

Using the Pythagoras Theorem, the distance of z from the origin, or the magnitude of z, is

\[\left| z \right| = \sqrt {{{\left( { - 2} \right)}^2} + {{\left( {2\sqrt 3 } \right)}^2}}  = \sqrt {16}  = 4\]

Now, let us calculate the angle between the line segment joining the origin to z (OP) and the positive real direction (ray OX). Note that the angle POX' is

\[\begin{array}{l}{\tan ^{ - 1}}\left( {\frac{{PQ}}{{OQ}}} \right) = {\tan ^{ - 1}}\left( {\frac{{2\sqrt 3 }}{2}} \right) = {\tan ^{ - 1}}\left( {\sqrt 3 } \right)\\ \qquad\qquad\qquad\qquad\qquad\;\;\,\,\,\,\,\,\,\,\,\, = {60^0}\end{array}\]

Thus, the argument of z (which is the angle POX) is

\[\arg \left( z \right) = {180^0} - {60^0} = {120^0}\]

It is easy to see that for an arbitrary complex number \(z = x + yi\), its modulus will be

\[\left| z \right| = \sqrt {{x^2} + {y^2}} \]

To determine the argument of z, we should plot it and observe its quadrant, and then accordingly calculate the angle which the line joining the origin to z makes with the positive Real direction.

Example 1: Determine the modulus and argument of \(z = 1 + 6i\).

Solution: We have:

\[\left| z \right| = \sqrt {{1^2} + {6^2}}  = \sqrt {37} \]

Now, the plot below shows that z lies in the first quadrant:

Clearly, the argument of z is given by

\[\arg \left( z \right) = \theta  = {\tan ^{ - 1}}\left( {\frac{6}{1}} \right) = {\tan ^{ - 1}}6\]

Example 2: Find the modulus and argument of \(z = 1 - 3i\).

Solution: The modulus is

\[\left| z \right| = \sqrt {{1^2} + {{\left( { - 3} \right)}^2}}  = \sqrt {10} \]

Now, we see from the plot below that z lies in the fourth quadrant:

The angle \(\theta \) is given by

\[\theta  = {\tan ^{ - 1}}\left( {\frac{3}{1}} \right) = {\tan ^{ - 1}}3\]

Can we say that the argument of z is \(\theta \)? Well, since the direction of z from the Real direction is \(\theta \) measured clockwise (and not anti-clockwise), we should actually specify the argument of z as \( - \theta \):

\[\arg \left( z \right) =  - \theta  =  - {\tan ^{ - 1}}3\]

The significance of the minus sign is in the direction in which the angle needs to be measured. The following example clarifies this further.

Example 3:  Find the moduli (plural of modulus) and arguments of \({z_1} = 2 + 2i\) and \({z_2} = 2 - 2i\).

Solution: We have:

\[\begin{align}&\left| {{z_1}} \right| = \sqrt {{{\left( 2 \right)}^2} + {{\left( 2 \right)}^2}}  = \sqrt 8  = 2\sqrt 2 \\&\left| {{z_2}} \right| = \sqrt {{{\left( 2 \right)}^2} + {{\left( { - 2} \right)}^2}}  = \sqrt 8  = 2\sqrt 2 \end{align}\]

 The moduli of the two complex numbers are the same. This is evident from the following figure, which shows that the two complex numbers are mirror images of each other in the horizontal axis, and will thus be equidistant from the origin:

Now, we note that

\[{\theta _1} = {\theta _2} = {\tan ^{ - 1}}\left( {\frac{2}{2}} \right) = {\tan ^{ - 1}}1 = \frac{\pi }{4}\]

Thus,

\[\begin{align}&\arg \left( {{z_1}} \right) = {\theta _1} = \frac{\pi }{4}\\&\arg \left( {{z_2}} \right) =  - {\theta _2} =  - \frac{\pi }{4}\end{align}\]

We have seen examples of argument calculations for complex numbers lying the in the first, second and fourth quadrants. Let us see how we can calculate the argument of a complex number lying in the third quadrant.

Example 4: Find the modulus and argument of \(z =  - 1 - i\sqrt 3 \).

Solution: The modulus of z is:

\[\left| z \right| = \sqrt {{{\left( { - 1} \right)}^2} + {{\left( { - \sqrt 3 } \right)}^2}}  = \sqrt 4  = 2\]

The plot below shows that z lies in the third quadrant:

The angle \(\theta \) is given by

\[\theta  = {\tan ^{ - 1}}\left( {\frac{{\sqrt 3 }}{1}} \right) = {\tan ^{ - 1}}\sqrt 3  = \frac{\pi }{3}\]

Thus, the angle between OP and the positive Real direction is

\[\phi  = \pi  - \theta  = \pi  - \frac{\pi }{3} = \frac{{2\pi }}{3}\]

Now, since the angle \(\phi \) sweeps in the clockwise direction, the actual argument of z will be:

\[\arg \left( z \right) =  - \phi  =  - \frac{{2\pi }}{3}\]

We could also have calculated the argument by calculating the magnitude of the angle sweep in the anti-clockwise direction, as shown below:

This way, we can write the argument is

\[\arg \left( z \right) = \pi  + \theta  = \pi  + \frac{\pi }{3} = \frac{{4\pi }}{3}\]

Both ways of writing the arguments are correct, since the two arguments actually correspond to the same direction.