Equivalent Fractions
Equivalent fractions can be defined as fractions that may have different numerators and denominators but they represent the same value. For example, 9/12 and 6/8 are equivalent fractions because both are equal to 3/4 when simplified.
All equivalent fractions get reduced to the same fraction in their simplest form as seen in the example given above. Explore the given lesson to get a better idea of how to find equivalent fractions and how to check if the given fractions are equivalent.
| 1. | What are Equivalent Fractions? |
| 2. | How to Find Equivalent Fractions? |
| 3. | How do you know if Two Fractions are Equivalent? |
| 4. | Equivalent Fractions Chart |
| 5. | FAQs on Equivalent Fractions |
What are Equivalent Fractions?
Two or more fractions are said to be equivalent if they are equal to the same fraction when simplified. For example, the equivalent fractions of 1/5 are 5/25, 6/30, and 4/20, which on simplification, result in the same fraction, that is, 1/5.
Equivalent Fractions Definition
Equivalent fractions are defined as those fractions which are equal to the same value irrespective of their numerators and denominators. For example, both 6/12 and 4/8 are equal to 1/2, when simplified, which means they are equivalent in nature.
Equivalent Fractions Examples
Here are some examples of equivalent fractions.
Example: 1/2, 2/4, 3/6, and 4/8 are equivalent fractions. Let us see how their values are equal. We will represent each of these fractions as circles with shaded parts. It can be seen that the shaded parts in all the figures represent the same portion if seen as a whole.
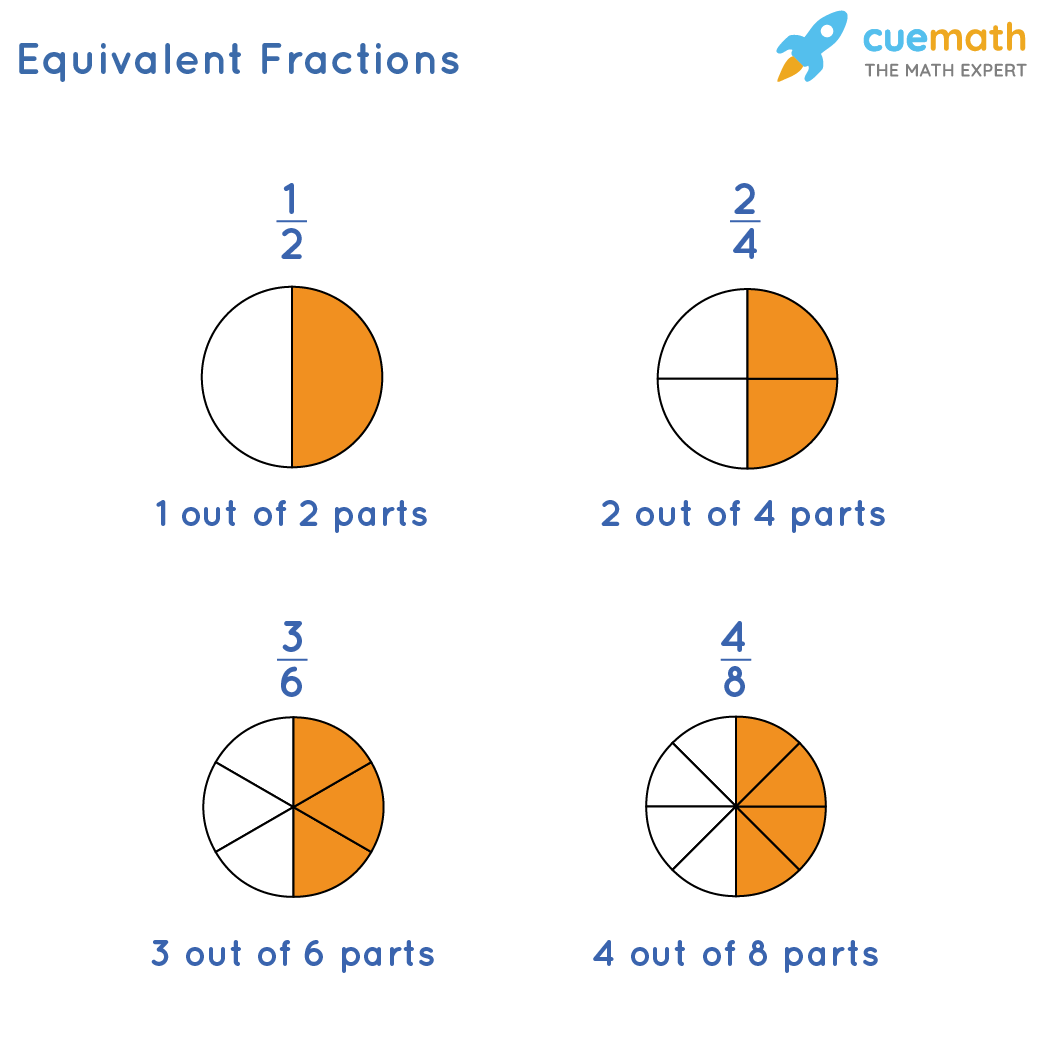
Here, we can see that the amount of shaded portion is the same in all the circles. Hence, 1/2, 2/4, 3/6, and 4/8 are equivalent fractions.
How to Find Equivalent Fractions?
Equivalent fractions can be written by multiplying or dividing both the numerator and the denominator by the same number. This is the reason why these fractions get reduced to the same number when they are simplified. Let us understand the two ways in which we can make equivalent fractions:
- Multiply the numerator and the denominator by the same number.
- Divide the numerator and the denominator by the same number.
Multiply the Numerator and Denominator by the Same Number
To find the equivalent fractions for any given fraction, multiply the numerator and the denominator by the same number. For example, to find an equivalent fraction of 3/4, multiply the numerator 3 and the denominator 4 by the same number, say, 2. Thus, 6/8 is an equivalent fraction of 3/4. We can find some other equivalent fractions by multiplying the numerator and the denominator of the given fraction by the same number.
- 3/4= \(\dfrac{3 \times 3}{4 \times 3}\) =9/12
- 3/4=\(\dfrac{3 \times 4}{4 \times 4}\) =12/16
- 3/4=\(\dfrac{3 \times 5}{4 \times 5}\) =15/20
Thus, the equivalent fractions of 3/4 are 6/8, 9/12, 12/16, and 15/20.
Divide the Numerator and Denominator by the Same Number
To find the equivalent fractions for any given fraction, divide the numerator and the denominator by the same number. For example, to find an equivalent fraction of 72/108, we will first find their common factors. We know that 2 is a common factor of both 72 and 108. Hence, an equivalent fraction of 72/108 can be found by dividing its numerator and denominator by 2. Thus, 36/54 is an equivalent fraction of 72/108. Let us see how the fraction is further simplified:
- 2 is a common factor of 36 and 54. Thus, 36/54= \(\dfrac{36 \div 2}{54 \div 2}\)= 18/27
- Again, 3 is a common factor of 18 and 27. Thus, 18/27= \(\dfrac{18 \div 3}{27 \div 3}\)= 6/9
- Again, 3 is a common factor of 6 and 9. Thus, 6/9=\(\dfrac{6 \div 3}{9 \div 3}\)= 2/3
Therefore, a few equivalent fractions of 72/108 are 36/54, 18/27, 6/9, and 2/3. Here, 2/3 is the simplified form of 72/108 as there is no common factor (other than 1) of 2 and 3.
How do you know if Two Fractions are Equivalent?
We need to simplify the given fractions to find whether they are equivalent or not. Simplification to get equivalent numbers can be done to a point where both the numerator and denominator should still be whole numbers. There are various methods to identify if the given fractions are equivalent. Some of them are as follows:
- Making the denominators the same.
- Finding the decimal form of both the fractions.
- Cross multiplication method.
- Visual method.
Let us identify whether 2/6 and 3/9 are equivalent fractions by each of these methods.
Making the Denominators the Same
The denominators of the fractions, 2/6 and 3/9 are 6 and 9. The Least Common Multiple (LCM) of the denominators 6 and 9 is 18. Let us make the denominators of both fractions 18, by multiplying them with suitable numbers.
- 2/6=\(\dfrac{2 \times 3}{6 \times 3}\)= 6/18
- 3/9=\(\dfrac{3 \times 2}{9 \times 2}\)= 6/18
We can observe that both the fractions are equivalent to the same fraction 6/18. Thus, the given fractions are equivalent.
Note: If the fractions are NOT equivalent, we can check the greater or smaller fraction by looking at the numerator of both the resultant fractions. Hence, this method can also be used for comparing fractions.
Finding the Decimal form of Both the Fractions
Let us find the decimal form of both the fractions 2/6 and 3/9 to see if they give the same value.
- 2/6= 0.3333333...
- 3/9= 0.3333333...
The decimal values of both the fractions are the same and hence, they are equivalent.
Cross Multiplication Method
To identify whether 2/6 and 3/9 are equivalent, we cross multiply them. If both the products are the same, the fractions are equivalent.

Since both the products here are 18, the given fractions are said to be equivalent fractions.
Visual Method
Let us represent each of the fractions 2/6 and 3/9 pictorially on identical shapes and check if the shaded portions of both are equal.

We can see that the shaded portions of both the circles depict the same value. In other words, it can be seen that the shaded parts in both the figures represent the same portion if seen as a whole. Hence, the given fractions are equivalent.
Equivalent Fractions Chart
Charts and tables are often used to represent concepts in a better way since they serve as a handy reference for calculations and are easier to understand. Anchor charts and tables, like the one given below, make it easier for the students to understand equivalent fractions. Let us use the following chart to find the equivalent fractions of 1/4.

From this chart, we can observe that the equivalent fractions of 1/4 are: 2/8, 3/12, 4/16,...
Tips on Equivalent Fractions
- Two fractions are said to be equivalent if their values (decimal value/graphical value) are the same.
- We usually multiply the numerator and denominator of a fraction by the same number to get its equivalent fraction.
- The 'Cross multiplication method' is used to determine whether any two fractions are equivalent or not.
- 'Making the denominators the same' is another method used to determine if two or more fractions are equivalent.
☛ Related Articles
Equivalent Fractions Examples
-
Example 1: Are 12/20 and 22/30 equivalent fractions?
Solution:
Method 1:
To check if the given fractions are equivalent, we will make the denominators the same by multiplication. The denominators of the fractions 12/20 and 22/30 are 20 and 30. The LCM of the denominators is 60. Let us make the denominators of both the fractions equal to 60, by multiplying them with the suitable numbers: 12/20=\(\dfrac{12 \times 3}{20 \times 3}\)= 36/60, 22/30=\(\dfrac{22 \times 2}{30 \times 2}\)= 44/60. Here, it can be seen that 36 is not equal to 44, that is 36 < 44. Therefore, 12/20 and 22/30 are not equivalent fractions.
Method 2:
This can be checked by the cross multiplication method. If we cross multiply the given fractions, we will get 20 × 22 = 440, and 12 × 30 = 360. We can see that 440 is not equal to 360. Therefore, 12/20 and 22/30 are not equivalent fractions.
-
Example 2: Find the equivalent fraction of 3/4 from the following:
a.) 6/8
b.) 6/12
Solution:
The equivalent fraction of 3/4 from the given fractions is 6/8 because when we reduce 6/8 to its lowest terms, we get 3/4.
-
Example 3: Check whether the given fractions are equivalent or not: 2/12 and 3/18
Solution: Let us check the equivalence of the given fractions by the cross multiplication method. If we cross multiply the given fractions, we will get 12 × 3 = 36, and 2 × 18 = 36. We can see that we get the same product, that is, 36. Therefore, 2/12 and 3/18 are equivalent fractions.

FAQs on Equivalent Fractions
What are Equivalent Fractions in Math?
Two or more fractions are said to be equivalent fractions if they are equal to the same value irrespective of their numerators and denominators. For example, 2/4 and 8/16 are equivalent fractions because they get reduced to 1/2 when simplified.
What are the Examples of Equivalent Fractions?
There can be many examples of equivalent fractions, like, 8/12 and 6/9 are equivalent fractions because they get reduced to the same fraction (2/3) when simplified. Similarly, 4/7 and 28/49 are also equivalent fractions.
How to Find Equivalent Fractions?
If the given fractions are simplified and they get reduced to a common fraction, then they can be termed as equivalent fractions. Apart from this, there are various other methods to identify whether the given fractions are equivalent or not. Some of them are as follows:
- Making the denominators the same.
- By finding the decimal form of both the fractions.
- Cross multiplication method.
- Visual method.
What does it Mean when Two Fractions are Equivalent?
When two fractions are equivalent, it means they are equal to the same value irrespective of their different numerators and denominators. In other words, when they are simplified they get reduced to the same fraction.
Why are Equivalent Fractions Important?
Equivalent fractions help us to add, subtract, multiply, divide fractions, and compare fractions which helps us solve many real-time problems.
What is an Equivalent Improper Fraction?
An equivalent improper fraction means an equivalent fraction in an improper form. A fraction is said to be improper when its numerator is greater than its denominator. For example, 3/2 is an improper fraction that is equivalent to 9/6.
How to Figure out Equivalent Fractions?
Any two fractions can be considered to be equivalent if they are equal to the same value. There are various methods to find out if the fractions are equivalent. The basic method is by reducing them. If they get reduced to the same fraction they are considered to be equivalent.
How to Write Equivalent Fractions?
Equivalent fractions can be written by multiplying or dividing both the numerator and the denominator by the same number. This is the reason why these fractions get reduced to the same number when they are simplified. For example, let us write an equivalent fraction for 2/3. We will multiply the numerator and denominator by 4 and we will get (2 × 4)/(3 × 4) = 8/12. Therefore, 8/12 and 2/3 are equivalent fractions.
Give 2 Equivalent Fractions for 6/8.
In order to write the equivalent fraction for 6/8, let us multiply the numerator and denominator by 2 and we will get (6 × 2)/(8 × 2) = 12/16. Therefore, 6/8 and 12/16 are equivalent fractions. Now, let us get another equivalent fraction for 6/8, by dividing it by a common number, say, 2. After dividing the numerator and denominator by 2 and we will get (6 ÷ 2)/(8 ÷ 2) = 3/4. Therefore, 6/8 and 3/4 are equivalent fractions.
What are the Equivalent Fractions of 1/4?
In order to find the equivalent fractions of 1/4, let us multiply the numerator and denominator by the same number. So, we will multiply it by 2 which will be, (1 × 2)/(4 × 2) = 2/8. Now, to find another equivalent fraction for 1/4, let us multiply it by 3. This will be, (1 × 3)/(4 × 3) = 3/12. So, we get two equivalent fractions for 1/4, and they are 2/8 and 3/12.
What is the Meaning of Equivalent Fractions?
Two or more fractions are said to be equivalent if they are equal to the same fraction when simplified. For example, the equivalent fractions of 1/6 are 2/12, 3/18, and 4/24, which on simplification, result in the same fraction, that is, 1/6.
What Fractions are Equivalent to 2/3?
In order to find the equivalent fractions of 2/3, let us multiply the numerator and denominator by the same number. So, we will multiply it by 5 which will be, (2 × 5)/(3 × 5) = 10/15. Now, to find another equivalent fraction for 2/3, let us multiply it by 6. This will be, (2 × 6)/(3 × 6) = 12/18. So, we get two equivalent fractions for 2/3, and they are 10/15 and 12/18.
What Fraction is Equivalent to 1/3?
In order to find the equivalent fractions of 1/3, let us multiply the numerator and denominator by the same number. So, we will multiply it by 2 which will be, (1 × 2)/(3 × 2) = 2/6. Now, to find another equivalent fraction for 1/3, let us multiply it by 3. This will be, (1 × 3)/(3 × 3) = 3/9. So, we get two equivalent fractions for 1/3, and they are 2/6 and 3/9.
What Fraction is Equivalent to 3/4?
In order to find the equivalent fractions of 3/4, let us multiply the numerator and denominator by the same number. So, we will multiply it by 2 which will be, (3 × 2)/(4 × 2) = 6/8. Now, to find another equivalent fraction for 3/4, let us multiply it by 3. This will be, (3 × 3)/(4 × 3) = 9/12. So, we get two equivalent fractions for 3/4, and they are 6/8 and 9/12.
What is the Equivalent Fraction of 3/5?
In order to find the equivalent fractions of 3/5, let us multiply the numerator and denominator by the same number. So, we will multiply it by 2 which will be, (3 × 2)/(5 × 2) = 6/10. Now, to find another equivalent fraction for 3/5, let us multiply it by 3. This will be, (3 × 3)/(5 × 3) = 9/15. So, we get two equivalent fractions for 3/5, and they are 6/10 and 9/15.
What Fraction is Equivalent to 1/2?
In order to find the equivalent fractions of 1/2, let us multiply the numerator and denominator by the same number. So, we will multiply it by 2 which will be, (1 × 2)/(2 × 2) = 2/4. Now, to find another equivalent fraction for 1/2, let us multiply it by 3. This will be, (1 × 3)/(2 × 3) = 3/6. So, we get two equivalent fractions for 1/2, and they are 2/4 and 3/6.
visual curriculum