Number Systems
Number systems are systems in mathematics that are used to express numbers in various forms and are understood by computers. A number is a mathematical value used for counting and measuring objects, and for performing arithmetic calculations. Numbers have various categories like natural numbers, whole numbers, rational and irrational numbers, and so on. Similarly, there are various types of number systems that have different properties, like the binary number system, the octal number system, the decimal number system, and the hexadecimal number system.
In this article, we will explore different types of number systems that we use such as the binary number system, the octal number system, the decimal number system, and the hexadecimal number system. We will learn the conversions between these number systems and solve examples for a better understanding of the concept.
What are Number Systems?
A number system is a system representing numbers. It is also called the system of numeration and it defines a set of values to represent a quantity. These numbers are used as digits and the most common ones are 0 and 1, that are used to represent binary numbers. Digits from 0 to 9 are used to represent other types of number systems.
Number Systems Definition
A number system is defined as the representation of numbers by using digits or other symbols in a consistent manner. The value of any digit in a number can be determined by a digit, its position in the number, and the base of the number system. The numbers are represented in a unique manner and allow us to operate arithmetic operations like addition, subtraction, and division.
Types of Number Systems
There are different types of number systems in which the four main types are as follows.
- Binary number system (Base - 2)
- Octal number system (Base - 8)
- Decimal number system (Base - 10)
- Hexadecimal number system (Base - 16)
We will study each of these systems one by one in detail after going through the following number system chart.
Number System Chart
Given below is a chart of the main four types of number system that we use to represent numbers.
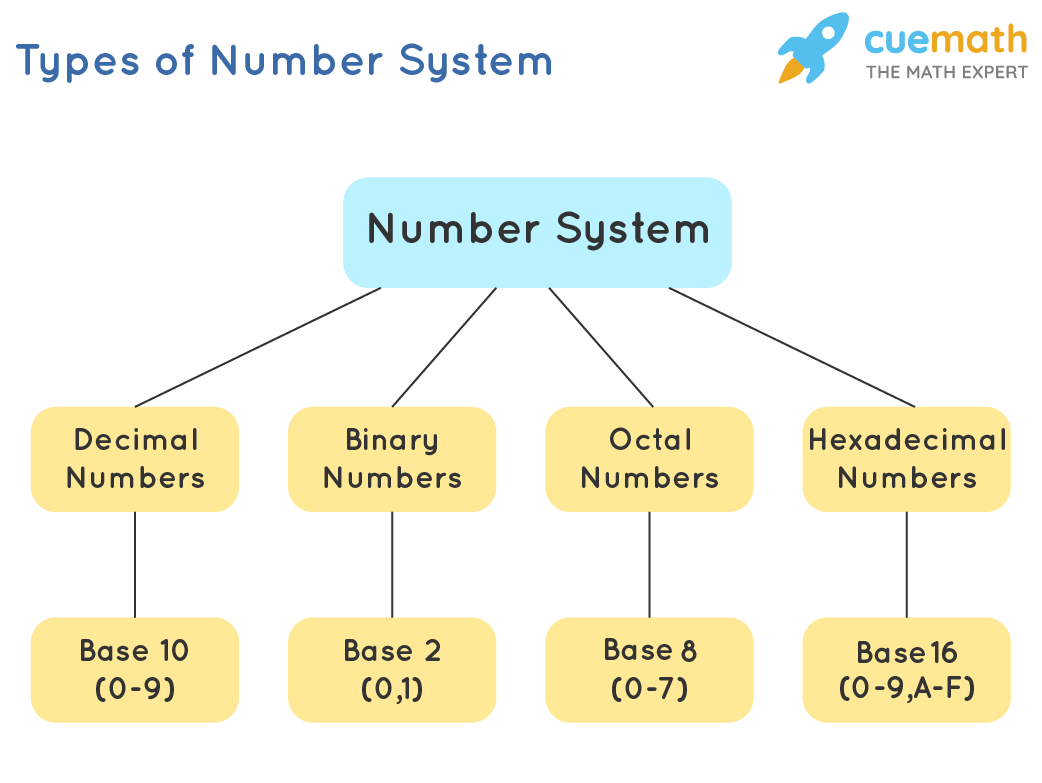
Binary Number System
The binary number system uses only two digits: 0 and 1. The numbers in this system have a base of 2. Digits 0 and 1 are called bits and 8 bits together make a byte. The data in computers is stored in terms of bits and bytes. The binary number system does not deal with other numbers such as 2,3,4,5 and so on. For example: 100012, 1111012, 10101012 are some examples of numbers in the binary number system.

Octal Number System
The octal number system uses eight digits: 0,1,2,3,4,5,6 and 7 with the base of 8. The advantage of this system is that it has lesser digits when compared to several other systems, hence, there would be fewer computational errors. Digits like 8 and 9 are not included in the octal number system. Just like the binary, the octal number system is used in minicomputers but with digits from 0 to 7. For example, 358, 238, and 1418 are some examples of numbers in the octal number system.

Decimal Number System
The decimal number system uses ten digits: 0,1,2,3,4,5,6,7,8 and 9 with the base number as 10. The decimal number system is the system that we generally use to represent numbers in real life. If any number is represented without a base, it means that its base is 10. For example, 72310, 3210, and 425710 are some examples of numbers in the decimal number system.

Hexadecimal Number System
The hexadecimal number system uses sixteen digits/alphabets: 0,1,2,3,4,5,6,7,8,9 and A,B,C,D,E,F with the base number as 16. Here, A-F of the hexadecimal system means the numbers 10-15 of the decimal number system respectively. This system is used in computers to reduce the large-sized strings of the binary system. For example, 7B316, 6F16, and 4B2A16 are some examples of numbers in the hexadecimal number system.

Conversion of Number Systems
A number can be converted from one number system to another number system using number system formulas. Like binary numbers can be converted to octal numbers and vice versa, octal numbers can be converted to decimal numbers and vice versa, and so on. Let us see the steps required in converting number systems.
Steps for Conversion of Binary to Decimal Number System
To convert a number from the binary to the decimal system, we use the following steps.
- Step 1: Multiply each digit of the given number, starting from the rightmost digit, with the exponents of the base.
- Step 2: The exponents should start with 0 and increase by 1 every time we move from right to left.
- Step 3: Simplify each of the above products and add them.
Let us understand the steps with the help of the following example in which we need to convert a number from binary to decimal number system.
Example: Convert 1001112 into the decimal system.
Solution:
Step 1: Identify the base of the given number. Here, the base of 1001112 is 2.
Step 2: Multiply each digit of the given number, starting from the rightmost digit, with the exponents of the base. The exponents should start with 0 and increase by 1 every time as we move from right to left. Since the base is 2 here, we multiply the digits of the given number by 20, 21, 22 , and so on from right to left.

Step 3: We just simplify each of the above products and add them.

Here, the sum is the equivalent number in the decimal number system of the given number. Or, we can use the following steps to make this process simplified.
100111 = (1 × 25) + (0 × 24) + (0 × 23) + (1 × 22) + (1 × 21) + (1 × 20)
= (1 × 32) + (0 × 16) + (0 × 8) + (1 × 4) + (1 × 2) + (1 × 1)
= 32 + 0 + 0 + 4 + 2 + 1
= 39
Thus, 1001112 = 3910.
Conversion of Decimal Number System to Binary / Octal / Hexadecimal Number System
To convert a number from the decimal number system to a binary/octal/hexadecimal number system, we use the following steps. The steps are shown on how to convert a number from the decimal system to the octal system.
Example: Convert 432010 into the octal system.
Solution:
Step 1: Identify the base of the required number. Since we have to convert the given number into the octal system, the base of the required number is 8.
Step 2: Divide the given number by the base of the required number and note down the quotient and the remainder in the quotient-remainder form. Repeat this process (dividing the quotient again by the base) until we get the quotient less than the base.

Step 3: The given number in the octal number system is obtained just by reading all the remainders and the last quotient from bottom to top.

Therefore, 432010 = 103408
Conversion from One Number System to Another Number System
To convert a number from one of the binary/octal/hexadecimal systems to one of the other systems, we first convert it into the decimal system, and then we convert it to the required systems by using the above-mentioned processes.
Example: Convert 10101111002 to the hexadecimal system.
Solution:
Step 1: Convert this number to the decimal number system as explained in the above process.

Thus, 10101111002 = 70010 → (1)
Step 2: Convert the above number (which is in the decimal system), into the required number system (hexadecimal).
Here, we have to convert 70010 into the hexadecimal system using the above-mentioned process. It should be noted that in the hexadecimal system, the numbers 11 and 12 are written as B and C respectively.

Thus, 70010 = 2BC16 → (2)
From the equations (1) and (2), 10101111002 = 2BC16
☛ Related Articles- Indian Numeral System
- International Number System
- Binary Calculator
- Binary to Octal Conversion
- Octal to Binary
- Decimal to Binary
- Binary to Decimal
- Decimal to Hexadecimal
- Hexadecimal to Decimal
Cuemath is one of the world's leading math learning platforms that offers LIVE 1-to-1 online math classes for grades K-12. Our mission is to transform the way children learn math, to help them excel in school and competitive exams. Our expert tutors conduct 2 or more live classes per week, at a pace that matches the child's learning needs.
Number Systems Examples
-
Example 1: Convert 30010 into the binary number system with base 2.
Solution: 30010 is in the decimal system. We divide 300 by 2 and note down the quotient and the remainder. We will repeat this process for every quotient until we get a quotient that is less than 2.

The equivalent number in the binary system is obtained by reading all the remainders and just the last quotient from bottom to top as shown above.
Thus, 30010 = 1001011002
-
Example 2: Convert 5BC16 into the decimal system.
Solution: 5BC16 is in the hexadecimal system. We know that B = 11 and C = 12 in the hexadecimal system. So we get the equivalent number in the decimal system using the following process:

Thus, 5BC16 = 146810
-
Example 3: Convert 1448 into the hexadecimal system.
Solution: The base of 1448 is 8. First, we will convert this number into the decimal system as follows:

Thus, 1448 = 10010 → (1). Now we will convert this into the hexadecimal system as follows:

Thus, 10010 = 6416 → (2)
From the equations (1) and (2), we can conclude that: 1448 = 6416

FAQs on Number Systems
What are Number Systems with Examples?
A number system is a system of writing or expressing numbers. In mathematics, numbers are represented in a given set by using digits or symbols in a certain manner. Every number has a unique representation of its own and numbers can be represented in the arithmetic and algebraic structure as well. There are different types of number systems that have different properties, like the binary number system, the octal number system, the decimal number system, and the hexadecimal number system. Some examples of numbers in different number systems are 100102, 2348, 42810, and 4BA16.
What are the Different Types of Number Systems?
There are four main types of number systems:
- Binary number system (Base - 2)
- Octal number system (Base - 8)
- Decimal number system (Base - 10)
- Hexadecimal number system (Base - 16)
What are the Conversion Rules of Number Systems?
To convert a number from binary/octal/hexadecimal system to a decimal number system, we use the following steps:
- Multiply each digit of the given number, starting from the rightmost digit, with the exponents of the base.
- The exponents should start with 0 and increase by 1 every time we move from right to left.
- Simplify each of the above products and add them.
To convert a number from decimal system to binary/octal/hexadecimal system, we use the following steps:
- Divide the given number by the base of the required number and note down the quotient and the remainder in the “quotient-remainder” form.
- Repeat this process (dividing the quotient again by the base) until we get the quotient less than the base.
- The given number in the decimal number system is obtained just by reading all the remainders and the last quotient from bottom to top.
To convert a number from one of the binary/octal/hexadecimal systems to one of the other systems:
- We first convert it into the decimal system.
- Then we convert it to the required system.
What are the Uses of Each Number System?
There are different purposes of each number system, such as:
- The binary number system is used to store the data in computers.
- The advantage of the octal number system is that it has fewer digits when compared to several other systems, hence, there would be fewer computational errors.
- The decimal number system is the system that we use in daily life.
- The hexadecimal number system is used in computers to reduce the large-sized strings of the binary system.
What is the Importance of Number Systems?
Number systems help in representing the numbers in a small symbol set. Binary numbers are mostly used in computers that use digits like 0 and 1 for calculating simple problems. The number systems also help in converting one number system to another.
How are Number Systems Classified?
The number systems can be classified mainly into two categories: Positional and Non-positional number systems. For positional number systems, each digit is associated with a weight and its examples are binary, octal, decimal, etc. In non-positional number systems, the digit values are independent of their positions and its examples are gray code, cyclic code, aroma code, etc.
Why are Different Number Systems Used in Computers?
Computers cannot understand human languages, so to understand the commands and instructions given to the computers by programmers, different number systems are used such as the binary system, the octal system, the decimal system, and so on.
visual curriculum