Numbers up to 4 Digits
The 4-digit number series begins with the number 1,000 and ends with the number 9,999. 4-digit numbers are the numbers having 4-digits and we can form 4-digit numbers by using any digits from 0-9, but the number should begin with digit 1 or a number greater than 1. Numbers are categorized according to the number of digits that they have and the place value of a number helps in understanding the value of each digit.
| 1. | What are 4-Digit Numbers? |
| 2. | How to Write Numbers up to 4-Digits? |
| 3. | How to Decompose Numbers up to 4-Digits? |
| 4. | Tips and Tricks on Numbers up to 4-Digits |
| 5. | FAQs on Numbers up to 4-Digits |
What are 4-Digit Numbers?
4-digit numbers are those numbers that consist of only 4 digits in which the first digit should be 1 or greater than 1 and the rest of the digits can be any number between 0 and 9. For example, 5693, 1023, and 9825 are four-digit numbers.
How to Write Numbers up to 4-Digits?
4-digit numbers are written or read according to the place values of the digits. In 4 digit numbers, the four digits correspond to the four place values - ones, tens, hundreds, and thousands. When a number is written in standard form, each group of digits is separated by a comma which forms a period. The first period which is known as the 'ones period' is formed with the first three digits of the number, when counted from the right hand side. It should be noted that the placement of commas starts with 4 digit numbers. We put a comma just before the hundreds place because the first-period (ones) ends and the second period of thousands begins. For example, 3210 is a 4-digit number and after placing the comma, it is written as 3,210.
The smallest 4-digit number is 1,000 and the largest 4-digit number is 9,999, and there are a total of 9000 numbers from 1000 to 9999. We can make many four-digit numbers by using digits from 0 to 9 but we need to remember that the thousands place in a 4-digit number should not be 0. For example, 0875 is not a four-digit number, the number is considered as a three-digit number, that is, 875.
4-digit numbers can be written in three forms, i.e., in the numeral form, in words, and in the expanded form. For example, 2345 is a 4-digit number. In the numeral form, it is written as 2,345. In words, it is written as: Two thousand three hundred forty-five. In the expanded form it is written as: 2000 + 300 + 40 + 5, or, 2 thousands + 3 hundreds + 4 tens + 5 ones.
How to Decompose Numbers up to 4-Digits?
As already discussed above, a 4 digit number has the following place values - Thousands, Hundreds, Tens, and Ones. To decompose 4-digit numbers we multiply each digit of the 4-digit number with its value, that is, 1000, 100, 10, and 1 respectively. For example, the given 4-digit number 5627 can be decomposed as follows:
- 5 is at thousands place and its place value is 5 × 1000 = 5000
- 6 is at hundreds place and its place value is 6 × 100 = 600
- 2 is at tens place and its place value is 2 × 10 = 20
- 7 is at ones place and its place value is 7 × 1 = 7
So, the expanded form of 5627 = 5000 + 600 + 20 + 7
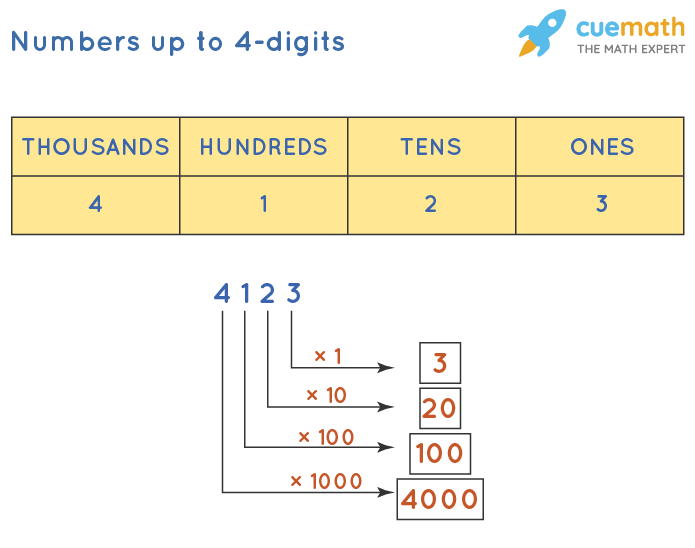
Observe the following figure which shows how to write a 4-digit number according to its place values. In this case, we have taken the example of a 4-digit number: 4,123. Here, 4 is written at the thousands place, 1 is written at the hundreds place, 2 is written at the tens place and 3 is written at ones place.
Tips and Tricks on Numbers up to 4-Digits
Given below are some of the tips and tricks on numbers up to 4 digits that can help while solving problems related to these numbers.
- When any one-digit number (from 1 to 9) is multiplied by 1000, the resultant number is a 4-digit number. For example, 5 × 1000 = 5,000
- When any two-digit number is multiplied by 100, the resultant number is a 4-digit number. For example, 44 × 100 = 4,400
- When any three-digit number is multiplied by 10, the resultant number is a 4-digit number. For example, 678 × 10 = 6,780
- When any four-digit number is multiplied by 1, the resultant number is a 4-digit number. For example, 2345 × 1 = 2345
- The smallest four-digit number, using all different digits, is 1023.
- The smallest four-digit number, using only one digit is 1,111.
- The smallest four-digit number, using two different digits is 1,000. (1,000 is the least four-digit number too).
- The greatest four-digit number, using only one digit is 9,999 (9,999 is the greatest four-digit number too).
- The greatest four-digit number, using two different digits is 9,998.
- The greatest four-digit number, using all different digits is 9,876.
Important Notes
Given below are some important notes related to numbers up to 4-digits that we studied in this article.
- There are 4 numbers (any number from 0-9) in a 4-digit number and the starting number should be 1 or greater than 1.
- The thousands place in a 4-digit number cannot be 0.
- The smallest 4-digit number is 1000 and the greatest 4-digit number is 9999.
- There are 9000 four-digit numbers in all.
Smallest 4 Digit Number
The smallest 4-digit number is 1000 because its predecessor is 999 which is a 3-digit number. 4-digit numbers start from 1000 and end on 9999.
Greatest 4 Digit Number
The greatest 4-digit number is 9999 because its successor is 10000 which is a 5-digit number. 4-digit numbers start from 1000 and end on 9999.
☛ Related Articles
Examples on Numbers Up to 4 Digits
-
Example 1: Write the greatest and the smallest 4-digit number using all the digits 1, 2, 3, 4.
Solution: Using the given numbers, the greatest 4-digit number is 4,321 and the smallest 4-digit number is 1,234.
-
Example 2: Write the greatest and the smallest 4-digit number using all the digits 1, 8, 5 (repetition allowed).
Solution: The greatest 4-digit number is 8,851. (Used all the digits and the repeated the digit 8)
The smallest 4-digit number is 1,158. (Used all the digits and the repeated the digit 1)
-
Example 3: The largest 4-digit number exactly divisible by 88 is ____.
Solution: The largest 4-digit number which is exactly divisible by 88 is 9944 because when we know that the largest 4-digit number is 9999 and when we divide 9999 by 88 we get 55 as the remainder. Now, if we subtract 55 from 9999, we get, 9999 - 55 = 9944.

FAQs on Numbers up to 4-Digits
What are 4-Digit Numbers?
In simple words, a number with 4-digits is a 4 digit number. The first digit of a 4-digit number should be 1 or greater than one and the remaining digits can be any number from 0 to 9. Four-digit numbers start from 1000 and end at 9999. The place values in a 4 digit number, starting from the right, are ones, tens, hundreds, and thousands.
What is the Largest 4-digit Number?
9,999 is the largest 4-digit number. We can read the number in words as nine thousand nine hundred ninety-nine. The number after 9,999 is 10,000 and it is a five-digit number, therefore, the largest 4-digit number is 9,999.
What is the Smallest 4-digit Number?
1,000 is the smallest 4-digit number. We can read the number in words as one thousand. The number before 1,000 is 999 and it is a three-digit number, therefore, the smallest 4-digit number is 1,000.
How many 4-digit Numbers are there?
There are 9000, 4-digit numbers, and they start from the number 1000 and end on the number 9,999.
How to put a Comma in 4-Digit Numbers?
In 4 digit numbers, the 4th digit on the extreme left represents the thousands place. The comma in a 4-digit number is placed between the 4th digit and the 3rd digit, from the right, that is, in between the thousands place and the hundreds place. For example, the 4 digit number 3674 is written as 3,674.
What are the Prime Factors of the Greatest 4 Digit Number?
The prime factors of the greatest 4-digit number, 9999 are 3, 11, and 101.
Which is the Greatest 4 Digit number which is a Perfect Square?
The greatest 4-digit number which is a perfect square is 9801.
visual curriculum