Examples On Exact Differential Equations

Example – 16

Solve the DE \(2xydx + ({x^2} + 3{y^2})dy = 0.\)

Solution: First of all, notice that this DE is homogeneous :

\[\frac{{dy}}{{dx}} = - \frac{{2xy}}{{{x^2} + 3{y^2}}}\]

The substitution \(y = vx\) leads to

\[\begin{align} &\qquad\;\;  v + x\frac{{dv}}{{dx}} = \frac{{ - 2v{x^2}}}{{{x^2} + 3{v^2}{x^2}}} = \frac{{ - 2v}}{{1 + 3{v^2}}}\\&\Rightarrow \quad x\frac{{dv}}{{dx}} = - v - \frac{{2v}}{{1 + 3{v^2}}}\\ &\qquad\qquad\;\;= \frac{{ - 3v - 3{v^3}}}{{1 + 3{v^2}}}\\ &\qquad\qquad\;\; = \frac{{ - 3v(1 + {v^2})}}{{1 + 3{v^2}}}\\&\Rightarrow \quad \frac{{1 + 3{v^2}}}{{v(1 + {v^2})}}dv = - 3\frac{{dx}}{x}\end{align}\]

The substitution \({v^2} = t\) leads to

\[\begin{align} & \left( {\frac{{1 + 3t}}{{1 + t}} \cdot \frac{1}{{2t}}} \right)dt = - 3\frac{{dx}}{x}\\&\Rightarrow \quad \left( {\frac{1}{{1 + t}} + \frac{1}{{2t}}} \right)dt = - 3\frac{{dx}}{x}\end{align}\]

Integrating both sides gives

\[\begin{align}&\;\ln (1 + t) + \frac{1}{2}\ln t = - 3\ln x + \ln C\\& \Rightarrow \quad \sqrt t (1 + t){x^3} = C\\&\Rightarrow \quad v(1 + {v^2}){x^3} = C\\&\Rightarrow \quad y({x^2} + {y^2}) = C\end{align}\]

We now solve this DE again using the exact differential approach since by observation this DE satisfies the required criterion for it to be exact.

We have,

\[\frac{{\partial f}}{{\partial x}} = M = 2xy, \quad \frac{{\partial f}}{{\partial y}} = N = {x^2} + 3{y^2}\]

Integrating the first relation, we have

\[f(x,\,y) = {x^2}y + \phi (y) \qquad \ldots (1)\]

Differentiating this w.r.t. y and comparing with the expression for \(\begin{align}\frac{{\partial f}}{{\partial y}}\end{align}\) above, we have

\[\begin{align} & \qquad \frac{{\partial f}}{{\partial y}} = {x^2} + \phi '(y) = {x^2} + 3{y^2}\\&\Rightarrow \quad \phi '(y) = 3{y^2}\\&\Rightarrow \quad \phi (y) = {y^3} + C' & & & \ldots (2)\end{align}\]

Thus, from (1) and (2),

\[f(x,\,y) = {x^2}y + {y^3} + C'\]

The solution to the exact DE is

\[\begin{align} & \qquad \;\; f(x,\,y) = {\rm{constant}}\\&\Rightarrow \quad {x^2}y + {y^3} = C\\&\Rightarrow \quad y({x^2} + {y^2}) = C\end{align}\]

which is the same as the one obtained earlier. Thus, the exact differential approach might lead to the solution faster than the other approaches we’ve discussed earlier.

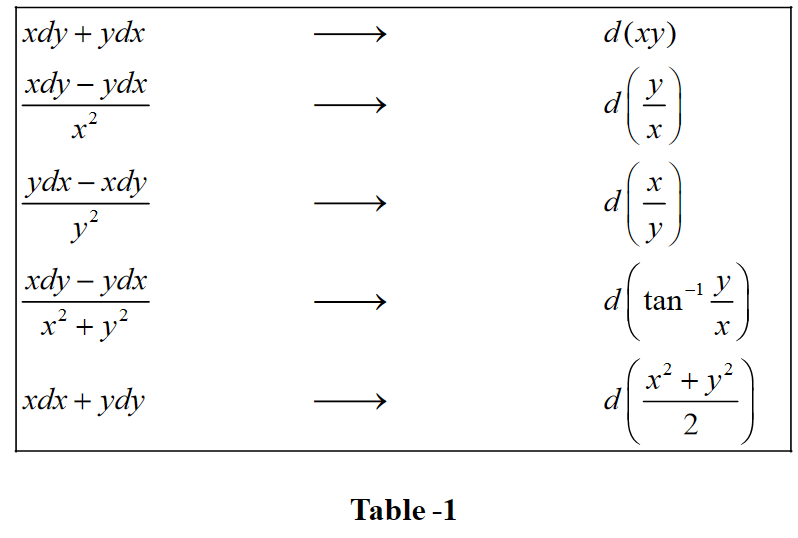
Sometimes, the fact that the DE is exact is evident merely be inspection. We list down such exact differentials (verify the truth of these relations):

Example – 17

Solve the DE\(\begin{align}\frac{{xdy}}{{{x^2} + {y^2}}} = \left( {\frac{y}{{{x^2} + {y^2}}} - 1} \right)dx.\end{align}\)

Solution: Upon rearrangement, this DE gives

\[\frac{{xdy - ydx}}{{{x^2} + {y^2}}} = - dx \qquad \qquad \cdots (1)\]

From Table-1, the L.H.S of (1) is the exact differential \(d\left( {{{\tan }^{ - 1}}\frac{y}{x}} \right).\) Thus, our DE reduces to \(d\left( {{{\tan }^{ - 1}}\frac{y}{x}} \right) + dx = 0\)

Integrating, we obtain the solution as

\[{\tan ^{ - 1}}\frac{y}{x} + x = C\]

However, it is very likely that we won’t be able to make out just be inspection whether the DE is exact or not.

If the DE is not exact, it can be rendered exact by multiplying it with an integrating factor I.F. In the case of the first-order linear DE

\[\frac{{dy}}{{dx}} + Py = Q\]

the I.F. \({e^{\int {Pdx} }}\) renders the DE exact:

\[\frac{d}{{dx}}\left( {y{e^{\int {Pdx} }}} \right) = Q{e^{\int {Pdx} }}\]

and the solution is now obtainable by integration.

If fact, a systematic approach exists to determine the I.F. in a general case (if such an I.F. is possible at all.). However, we’ll not be discussing that approach here since it is beyond our current scope.

Let us see another example, where the solution is easily obtained by the recognition of exact differentials present in the equation.

Example – 18

Solve the DE \(\begin{align}x\cos \left( {\frac{y}{x}} \right)\left( {ydx + xdy} \right) = y\sin \left( {\frac{y}{x}} \right)\left( {xdy - ydx} \right).\end{align}\)

Solution: Upon rearrangement, we have

\[\begin{align}&\qquad \;\;ydx + xdy = \frac{y}{x}\tan \frac{y}{x}\left( {xdy - ydx} \right)\\ &\qquad \qquad \quad  \qquad \;= xy\tan \frac{y}{x}\left( {\frac{{xdy - ydx}}{{{x^2}}}} \right)\\&\Rightarrow \quad \frac{{ydx + xdy}}{{xy}} = \tan \frac{y}{x}\left( {\frac{{xdy - ydx}}{{{x^2}}}} \right)\end{align}\]

From Table-1 this can be written as

\[\frac{{d(xy)}}{{xy}} = \tan \left( {\frac{y}{x}} \right)d\left( {\frac{y}{x}} \right)\]

The solution is now obtained simply by integrating both sides :

\[\begin{array}{l} & \ln (xy) = \ln \left( {\sec \left( {\frac{y}{x}} \right)} \right) + \ln C\\ \Rightarrow & xy = C\sec \left( {\frac{y}{x}} \right)\end{array}\]

TRY YOURSELF - II

Solve the following DEs:

Q. 1  \(\begin{align}xdx + ydy = a({x^2} + {y^2})dy\end{align}.\)

Q. 2  \(\begin{align}(3xy + {y^2})dx + ({x^2} + xy)dy = 0\end{align}.\)

Q. 3  \(\begin{align}\frac{{dy}}{{dx}} = \frac{{2x - y + 3}}{{x + 2y + 4}}\end{align}.\)

Q. 4   \(\begin{align}\frac{{dy}}{{dx}} + y\cot x = \cos x\end{align}.\)

Q. 5   \(\begin{align}x\frac{{dy}}{{dx}} - y = {y^3}\ln x\end{align}.\)