Excircle Formulae

Let us now turn our attention to excircles. For any triangle \(\Delta ABC\) , there will be three ex-circles. For examples, the ex-circle opposite to the angle A will touch the side BC and two sides AB and AC produced:

The ex-circle opposite to the angle A. The radius of this circle will be denoted by r₁. Similarly, the radii of the other two circles are denoted by r₂ and r₃.

The next four relations are concerned with the ex-radii  \({r_1},{r_2},{r_3}\)  and how these relate to the other parameters of the triangle:

\[\boxed{\begin{align}  & \ {{r}_{1}}=\frac{\Delta }{s-a},  &  &{{r}_{2}}=\frac{\Delta }{s-b},&    &{{r}_{3}}=\frac{\Delta }{s-c}\  \\  & \ {{r}_{1}}=s\tan \frac{A}{2},  &  &{{r}_{2}}=s\tan \frac{B}{2},&    &{{r}_{3}}=s\tan \frac{C}{2}\  \\ & \ {{r}_{1}}=\frac{a\cos \frac{B}{2}\cos \frac{C}{2}}{\cos \frac{A}{2}},&    &{{r}_{2}}=\frac{b\cos \frac{C}{2}\cos \frac{A}{2}}{\cos \frac{B}{2}},&    &{{r}_{3}}=\frac{c\cos \frac{A}{2}\cos \frac{B}{2}}{\cos \frac{C}{2}}\  \\  & \ {{r}_{1}}=4R\sin \frac{A}{2}\cos \frac{B}{2}\cos \frac{C}{2},&   &{{r}_{2}}=4R\cos \frac{A}{2}\sin \frac{B}{2}\cos \frac{C}{2},&    &{{r}_{3}}=4R\cos \frac{A}{2}\cos \frac{B}{2}\sin \frac{C}{2} \end{align}}\]

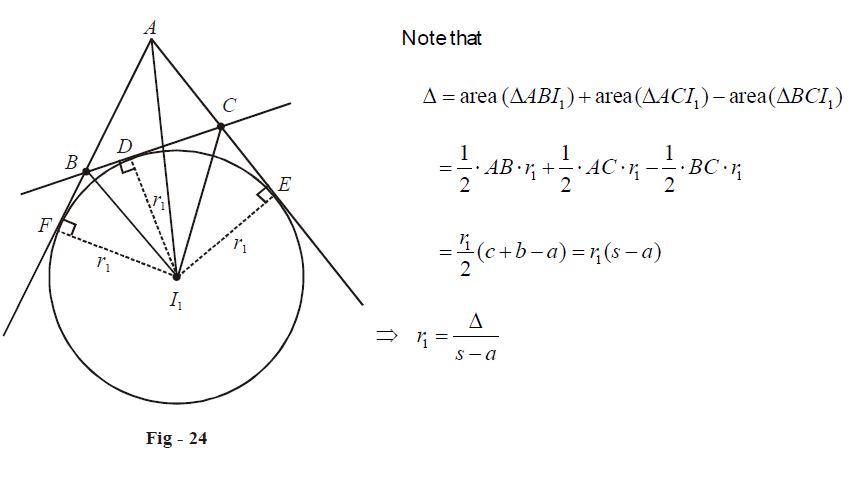
Let us justify the first of each set of relations.

Similarly, \(\begin{align}{r_2} = \frac{\Delta }{{s - b}}\;{\text{and}}\;{r_3} = \frac{\Delta }{{s - c}}\end{align}\)

Now, let us consider the second set of relations. In  \(\Delta AFI\)  , we’ll have  \({r_1} = AF\tan \frac{A}{2}\) . We need to prove that AF = s. To that end;

Thus,  \(\begin{align}{r_1} = s\tan \frac{A}{2}\end{align}\)  . Similarly, we can show that  \(\begin{align}{{r}_{2}}=s\tan \frac{B}{2}\;\;\;and\;\;\;{{r}_{3}}=s\tan \frac{C}{2}\text{ }\!\!~\!\!\text{ }.\end{align}\)

To prove the third set of relations, we note from  \(\Delta {I_1}BD\)  and  \(\Delta {I_1}CD\)  that

\[\begin{align}&\;\;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,BD = {r_1}\tan \frac{B}{2},\;\;\;\;\;DC = {r_1}\tan \frac{C}{2} & \left\{ {{\text{Justify}}\;{\text{these relations}}\;{\text{carefully}}} \right\} \\   &\Rightarrow\qquad   BD + DC = BC = a = {r_1}\left( {\tan \frac{B}{2} + \tan \frac{C}{2}} \right)  \\   &\Rightarrow\qquad   {r_1} = \frac{a}{{\tan \frac{B}{2} + \tan \frac{C}{2}}}  \\  \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, &\qquad\qquad\;= \frac{{a\cos \frac{B}{2}\cos \frac{C}{2}}}{{\sin \left( {\frac{{B + C}}{2}} \right)}}  \\  \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, &\qquad\qquad\;= \frac{{a\cos \frac{B}{2}\cos \frac{C}{2}}}{{\cos \frac{A}{2}}}  \\ \end{align} \]

Similar relations hold for \({r_2}\;{\text{and}}\;{r_3}\)  .

Finally, to prove the fourth set of relations, we use the relations  \(a = 2R\sin A\)  etc, so that

\[\begin{align}& {{r}_{1}}=\frac{2R\sin A\cos \frac{B}{2}\cos \frac{C}{2}}{\cos \frac{A}{2}} \\  &\quad =4R\sin \frac{A}{2}\cos \frac{B}{2}\cos \frac{C}{2} \end{align}\]

and similarly, for  \({r_2}\;{\text{and}}\;{r_3}\) .