Left Hand And Right Hand Derivatives

LEFT AND RIGHT DERIVATIVES

Let us now put the discussions we have done above in concrete mathematical form.

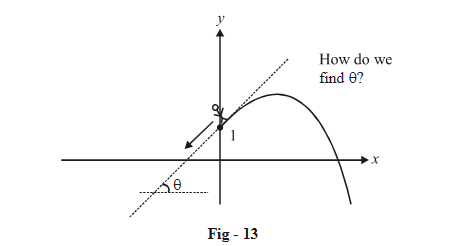
Consider the curve \(f\left( x \right){\rm{ }} = {\rm{ }}1{\rm{ }} + {\rm{ }}\left| x \right|{\rm{ }}-{x^2}\) .

Theta is walking on this curve towards the y-axis from the right. When he is infinitesimally close to the y-axis, his direction of travel will be along the tangent drawn to the right segment of the graph, at an x-coordinate in the immediate right neighbourhood of the origin; or equivalently, at a point on the right segment of the graph which is infinitesmally close to the point (0, 1).

How do we find out this direction of travel near the point (0, 1)? In other wards, how do we find out the slope of a tangent drawn to the right part of the graph, at a point extremely (infinitesmally) near to (0, 1)?

To evaluate this slope, we first drawn a secant on this graph, passing through (0, 1), as shown in the figure below:

Let the x-coordinate of the point Q be h. The slope of the secant PQ is

\[\begin{align}\tan \theta  = \frac{{QR}}{{PR}}\end{align}\]

Notice that QR is f (h) – f (0) and PR is h. Therefore,

\[\begin{align}\tan \theta = \frac{{f\left( h \right) - f\left( 0 \right)}}{h} \,\,\,\,\,\,\,\, ... \rm{(i)}\end{align}\]

Now we make this secant closer to a tangent by reducing h: look at the figure below; as h is reduced or as \(h \to 0\), the secant PQ ‘tends’ to become a tangent drawn ‘at’ P (or more accurately, a tangent at a point infinitesmally close to the point P):

We see that as the point \(Q \to P\)  or as \(h \to 0,\)  the secant PQ tends to become a tangent to the curve; to find the slope of this tangent, we find  \(\mathop {\lim }\limits_{h \to 0} \left( {\tan \theta } \right)\) where tan \(\theta\) is given by (i)

\[\begin{align}{\rm{Slope \,\,of \,\,tangent}} = \mathop {\lim }\limits_{h \to 0} \frac{{f\left( h \right) - f\left( a \right)}}{h}\end{align}\]

This limit gives us the slope of the tangent ‘at’ the point P. (By ‘at’ we mean ‘just near’). Lets evaluate this limit for this particular function:

\[\begin{align}f\left( x \right) &= 1 + \left| x \right| - {x^2}\\  \text{so }\qquad \qquad {\rm{ }}f\left( h \right) &= 1 + h - {h^2}\\
\text{and }\qquad \quad \;\;f\left( 0 \right) &= 1\\{\text{Slope of tangent}}& = \mathop {{\rm{lim}}}\limits_{{\rm{h}} \to {\rm{0}}} \frac{{f\left( h \right) - f\left( 0 \right)}}{h}\\&=\mathop {{\rm{lim}}}\limits_{{\rm{h}} \to {\rm{0}}} \frac{{h - {h^2}}}{h}\\ &= {\rm{ }}1\end{align}\]

This means that the tangent drawn at P (on the right part of the graph) is inclined at 45º to the x-axis.

In mathematical jargon, the limit we  have just evaluated is called the Right Hand Derivative (RHD) of f (x) at x = 0. This quantity, as we have seen, gives us the behaviour of the curve (its slope) in the immediate right side vicinity of x = 0.

Obviously, there will exist a Left  Hand Derivative (LHD) also that will give us the behaviour of the curve in the immediate left side vicinity of x = 0. In other words, the LHD will give us the direction of travel of Theta as he is ‘just about’ to reach the point (0, 1) travelling from the left towards the y-axis.

To evaluate the LHD, we follow a procedure similar to the one we used to evaluate the RHD; only this time we will drawn the secant PQ on the left side of the graph.

As the point \(Q \to P\)  or as \(h \to 0,\)  the secant PQ again tends to become a tangent. As for the previous case, the slope of this tangent will be given by;

\[\begin{align}\mathop {{\rm{Slope\,\, of\,\, tangent}}}\limits_{\left( {{\rm{LHD}}} \right)} \qquad \quad &= - \mathop {\lim }\limits_{h \to 0} \left( {\frac{{f\left( h \right) - f\left( 0 \right)}}{h}} \right)\,\,\,\,\,\,\,\,\,\,\,\,\,\left\{ {{\rm{why \,\,did\,\, we\,\, put\,\, a \,\,negative\,\, sign?}}} \right\}\\ &= \mathop {\lim }\limits_{h \to 0} \frac{{f\left( h \right) - f\left( 0 \right)}}{{ - h}}\\\text{For this particular case:}\\{\rm{LHD}} &= \mathop {\lim }\limits_{h \to 0} \frac{{\left( {1 + h - {h^2}} \right) - 1}}{{ - h}}\\&= - 1\end{align}\]

The tangent drawn to the left part of the graph ‘just near’ P will be inclined at 135º to the x-axis.

Notice that because there is a sharp point at x = 0, or in other words Theta’s direction of travel will change when crossing the y-axis, the LHD and RHD have different values. We would say that this function is  non-differentiable at x = 0.  No tangent can be drawn to f (x) precisely at x = 0.

On the other hand, for a ‘smooth’ function, the LHD and RHD at that point will be equal and such a function would be differentiable at that point. This means that a unique tangent can be drawn at that point.

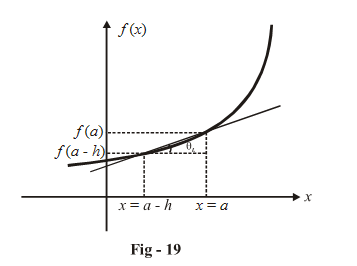
Before summarizing, let us write down the general expressions for the LHD and RHD

\(\boxed {\text{LHD at } x = a\\\text{for y} = f ( x ) }\)

\[\begin{align}&\tan \theta = \frac{{f\left( a \right) - f\left( {a - h} \right)}}{h} = \frac{{f\left( {a - h} \right) - f\left( a \right)}}{{ - h}}\\&
 \Rightarrow \qquad \boxed{{\text{LHD}}\left( {{\text{at }}x = a} \right) = \mathop {\lim }\limits_{h \to 0} \frac{{f\left( {a - h} \right) - f\left( a \right)}}{{ - h}}}\end{align}\]

\(\boxed{\text{RHD at }x = a\\\text{for y }= f ( x ) }\)

\[\begin{align}&\tan \theta = \frac{{f\left( {a + h} \right) - f\left( a \right)}}{h}\\&
\Rightarrow \qquad \boxed{{\text{RHD}}\left( {{\text{at }}x = a} \right) = \mathop {\lim }\limits_{h \to 0} \frac{{f\left( {a + h} \right) - f\left( a \right)}}{h}}\end{align}\]

To summarize:

Consider a continuous function y = f (x)

–       If at a particular point x = a, the LHD and RHD have equal numerical values, we say that f(x) is differentiable at x = a.In graphical terms, this means that the graph crosses x = a ‘smoothly’, without any sharp turn. This also means that a unique tangent can be drawn to the curve y = f (x)   at  x = a.

         The derivative at x = a implies the slope of the tangent at x = a ; i.e.

         Derivative (at x = a) = LHD = RHD

         {Obviously, the derivative exists only if f(x) is differentiable at x = a}

         The derivative at x = a is denoted by f '(a)

–       If at a particular point x = a, the LHD and RHD have non-equal values or one (or both) of them does not exist, we say that f(x) is non differentiable at x = a. Graphically, this means that the graph does not pass through x =  a ‘smoothly’, there is a sharp turn at x = a.

For a discontinuous function f(x) at x = a we can define LHD and RHD separately. We’ll soon see a few examples.

But for any discontinuous function at x = a,  f(x) would always be non differentiable at x = a since no unique tangent could be drawn to f(x) at x = a.

Therefore, for differentiability  at x = a the necessary and sufficient conditions that f (x) has to satisfy are:

(i)    f(x) must be continuous at x = a.

(ii)   LHD = RHD at x = a.