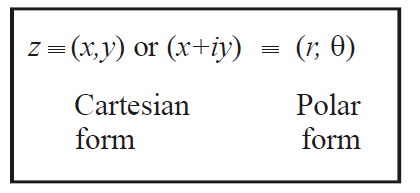Modulus And Argument Of Complex Numbers

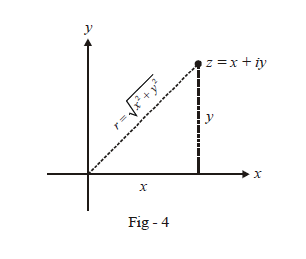
We will first define two useful quantities related to an arbitrary complex number \( z = x + iy. \)

 (\(a) \;\;\fbox{\({{\rm{Modulus:}}\,\,\,\,\,\left| z \right|}\)}\)

The modulus, which can be interchangeably represented by \(\left| z \right|\) or \(r,\) is the distance of the point \(z\) from the origin, so that its numerical value is given by \(\left| z \right| = r = \sqrt {{x^2} + {y^2}} \)

(b)  \(\fbox{\({{\rm{Argument:}}\,\,\,\,\,\arg \left( z \right)}\)}\)

The argument of \(z\) represented interchangeably by arg\((z)\) or \(\theta \)  , is the angle that the line joining \(z\) to the origin makes with the positive direction of the real axis. The argument of \(z\) can have infinite possible values; this is because if \(\theta \)  is an argument of \(z,\) then \(2n\pi  + \theta \)  is also a valid argument.

To be more specific, we define a unique value called the principal argument of \(z.\) The convention that is used to determine the principal argument for the four different quadrants in which \(z\) can lie, is depicted below:

Notice that Principal arg\(\left( z \right) \in \left( { - \pi ,\,\,\pi } \right]\) . For \(z\) above or on the real axis, principal arg \((z)\)\( \in \,\,[0,\,\pi ]\); it is non-negative and measured in the anti-clockwise direction from the positive real axis. For \(z\) below the real axis, principal arg\(\left( z \right) \in \left( { - \pi ,\,\,0} \right);\) it is negative and measured in a clockwise direction from the positive real axis.

From now on, arg\((z)\) will be considered to mean Principal arg\((z)\).

Observe now that we have two ways to specify an arbitrary complex number; one is the standard way \((x, y)\) which is referred to as the Cartesian form of the point. The second is by specifying the modulus and argument of \(z,\) instead of its \(x\) and \(y\) components  i.e., in the form \(\left( {r,\,\,\theta } \right)\) . This is referred to as the Polar form of the point.

Example - 1

Plot the following points on a plane and evaluate their polar forms:

(a) \(z = 1 + i\)	(b)  \(z =  - 1 + 2i\)
(c) \(z =  - 3 - 3i\)	(d) \(z = 3 - 4i\)
(e) \(z = 2i\)	(f) \(z = 3\)
(g) \(z =  - 4\)	(h)  \(z =  - 5i\)

Solution:  Observe the figures drawn for each of these parts carefully to determine how \(\left( {r,\,\,\theta } \right)\) is evaluated from  \(\left( {x,y} \right)\) or \(x + iy.\)  The polar forms so obtained are boxed.

Parts \((f)\) and \((g)\) above were included particularly so that you develop a tendency of thinking of even purely real numbers as points on the plane, and realise the fact that the real set \(\mathbb{R}\)  is just a subset of \(\mathbb{C}.\) 

Before moving to arithmetic operations on complex numbers, observe one more important relation between the cartesian and polar form of a complex number. You have seen how to write the polar form from the cartesian form. How do we do the reverse? This is quite straight forward:

Observe that \(AB = r\cos \theta \,\,\,{\rm{and}}\,\,\,BC = r\sin \theta \).

Therefore, the cartesian form is simply\(\left( {r\cos \theta ,\,\,r\sin \theta } \right)\) or \(r\cos \theta  + \,\,i\,r\sin \theta \) .

\[z = \left( {r,\theta } \right)\,\, \equiv \,\,\left( {r\cos \theta ,\,\,r\sin \theta } \right) \equiv r\left( {\cos \theta  + i\sin \theta } \right)\]

The representation

\[z = r\left( {\cos \theta  + i\sin \theta } \right)\]

is extremely useful, as we will soon see.

TRY YOURSELF - I

Q. 1  Plot the following complex numbers on a plane and evaluate their moduli and principal arguments.

(a)  \(z = 1 + 7i\)	(b) \(\begin{align}z =  - \frac{1}{2} + \frac{{\sqrt 3 }}{2}\;i\end{align}\) .
(c)  \(\begin{align}z = \frac{1}{{\sqrt 2 }} - \frac{1}{{\sqrt 2 }}i\end{align}\)	(d) \(z =  - 12 - 5\;i\)
(e) \(z = 6 - 7\;i\)	( f) \(\begin{align}z = {\left( {\frac{{i - 1}}{{i + 1}}} \right)^3}\end{align}\)

Q. 2  Evaluate  \({i^{996}} + {i^{.997}} + {i^{998}} + {i^{.999}}\)

Q. 3  For what smallest positive integral value of \(n\) is \(\begin{align}{\left( {\frac{{1 + i}}{{1 - i}}} \right)^n}\end{align}\) equal to 1 ?

Q. 4  What is the mistake in this computation?

\[1 = \sqrt 1  = \sqrt {( - 1) \times ( - 1)}  = \sqrt { - 1}  \times \sqrt { - 1}  = i \times i =  - 1\]