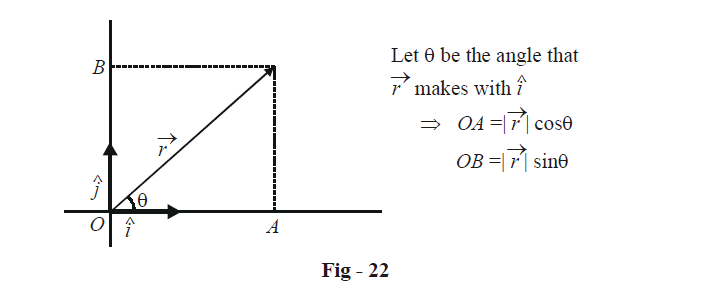Resolution Of Vectors

RESOLUTION OF A VECTOR IN A GIVEN BASIS

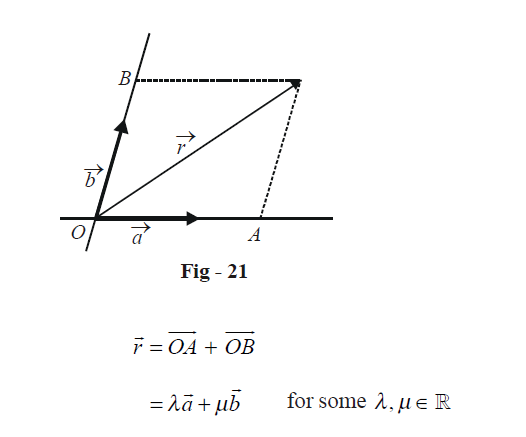
Consider two non-collinear vectors \(\vec a\,\,{\text{and}}\,\,\vec b\); as discussed earlier, these will form a basis of the plane in which they lie. Any vector  \(\vec r\) in the plane of \(\vec a\,\,{\text{and}}\,\,\vec b\) can be expressed as a linear combination of \(\vec a\,\,{\text{and}}\,\,\vec b\):

The vectors \(\overrightarrow {OA} \,\,\,{\text{and}}\,\,\overrightarrow {OB} \) are called the components of the vector \(\vec r\) along the basis formed by \(\vec a\,\,{\text{and}}\,\,\vec b\) . This is also stated by saying that the vector \(\vec r\) when resolved along the basis formed by \(\vec a\,\,{\text{and}}\,\,\vec b\) , gives the components  \(\overrightarrow {OA} \,\,\,{\text{and}}\,\,\overrightarrow {OB} \) . Also, as discussed earlier, the resolution of any vector along a given basis will be unique.

We can extend this to the three dimensional case: an arbitrary vector can be resolved along the basis formed by any three non-coplanar vectors, giving us three corresponding components. Refer to Fig - 20 for a visual picture.

RECTANGULAR  RESOLUTION

Let us select as the basis for a plane, a pair of unit vector \(\hat i\,\,{\text{and}}\,\,\hat j\) perpendicular to each other.

Any vector \(\vec r\) in this basis can be written as

\[\begin{align}&\vec r = \overrightarrow {OA}  + \overrightarrow {OB}  \hfill \\&\;= \left( {\left| {\vec r} \right|\cos \theta } \right)\hat i + \left( {\left| {\vec r} \right|\sin \theta } \right)\hat j \hfill \\&\;= x\hat i + y\hat j \hfill \\ 
\end{align} \]

where x and y are referred to as the x and y components of  \(\vec r\).

For 3-D space, we select three unit vectors \(\hat i,\hat j\,\,{\text{and}}\,\,\hat k\) each perpendicular to the other two.

In this case, any vector \(\vec r\) will have three corresponding components, generally denoted by x, y and z. We thus have

\[\vec r = x\hat i + y\hat j + z\hat k\]

The basis (\(\hat i,\hat j\)) for the two dimensional case and (\(\hat i,\hat j,\,\,\hat k\)) for the three-dimensional case are referred to as rectangular basis and are extremely convenient to work with. Unless otherwise stated, we’ll always be using a rectangular basis from now on. Also, we’ll always be implicitly assuming that we’re working in three dimensions since that automatically covers the two dimensional case.