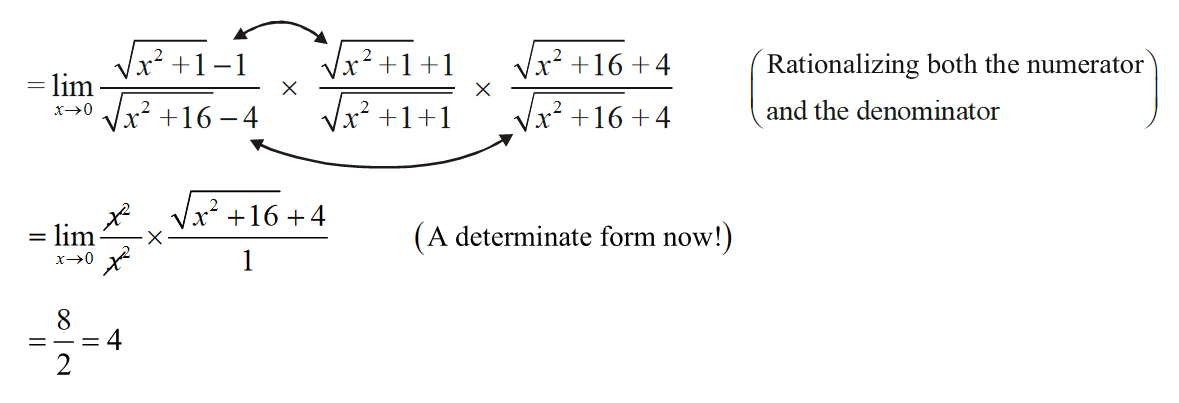Techniques Of Evaluating Limits

EVALUATION OF LIMITS:

Now we discuss the various methods used in obtaining limits. Each method will be accompanied by some examples illustrating that method.

(A)         DIRECT SUBSTITUTION

This already finds mention at the start of the current section, where we saw that for a continuous function, the limit can be obtained by direct substitution.

This is because, by definition of a continuous function (at x = a):

\({\text{LHL}}\;\left( {{\text{at}}\;\,x = a} \right) = {\text{RHL}}\;\left( {{\text{at}}\;\,x = a} \right)\; = f\left( a \right)\)

Hence, for example, all polynomial limits can be evaluated by direct substitution.

Some examples make all this clear:

(i)\(\mathop {\lim }\limits_{x \to 1} \,{x^3} + 1 = 2\)	(ii) \(\mathop {\lim }\limits_{x \to 2} \,\,5{x^2} + 3x + 1 = 27\)	(iii) \(\mathop {\lim }\limits_{x \to - 1} \,\,4{x^3} + 4 = 0\)
(iv) \(\mathop {\lim }\limits_{y \to 1} \,\,|y| + 1 = 2\)	(v) \(\mathop {\lim }\limits_{x \to 5} \,\,\frac{{5{x^2} + 4}}{{2x + 7}} = \frac{{129}}{{17}}\)	(vi) \(\mathop {\lim }\limits_{x \to 8} \,\,\frac{{{x^3} + 1}}{{x + 1}} = \frac{{513}}{9} = 57\)

and so on

(B) FACTORIZATION

We saw an example of this method in evaluating \(\begin{align}\mathop {\lim }\limits_{x \to 1} \frac{{{x^2} - 1}}{{x - 1}}\end{align}\) .

In such forms, the limit is indeterminate due to a certain factor occuring in the expression (For example, in the limit above, (x – 1) occurs in both the numerator and denominator and makes the limit indeterminate, of the form \(\frac{0}{0}\) ) . Factorization leads to cancellation of that common factor and reduction of the limit to a determinate form.

(i) \(\begin{align}\mathop {\lim }\limits_{x \to 1} \frac{{{x^3} - 1}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} \frac{{(x - 1)({x^2} + x + 1)}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} \left( {{x^2} + x + 1} \right) = 3\end{align}\)

   Note that this limit is also of the form \(\begin{align}\mathop {\lim }\limits_{x \to 1} \frac{{{x^m} - 1}}{{x - 1}}\end{align}\) (whose limit is m)

(ii) \(\begin{align}\mathop {\lim }\limits_{x \to 2} \frac{{{x^2} - 3x + 2}}{{{x^2} - 4}} = \mathop {\lim }\limits_{x \to 2} \frac{{(x - 1)(x - 2)}}{{(x - 1)(x + 2)}} = \mathop {\lim }\limits_{x \to 2} \frac{{x - 1}}{{x + 2}} = \frac{1}{4}\end{align}\)

(iii)  \(\begin{align}\mathop {\lim }\limits_{x \to 0} \frac{{(1 + x)(1 + 2x)(1 + 3x) - 1}}{x}\end{align}\)

             \( = \mathop {\lim }\limits_{x \to 0} \frac{{1 + 6x + 11{x^2} + 6{x^3} - 1}}{x}\) \(=\mathop {\lim }\limits_{x \to 0} \frac{{6x + 11{x^2} + 6{x^3}}}{x}\) \( = \mathop {\lim }\limits_{x \to 0} \,\,(6 + 11x + 6{x^2}) = 6\)

(iv) \(\begin{align}\mathop {\lim }\limits_{x \to 1} \,\,\frac{{{x^4} - 3x + 2}}{{{x^5} - 4x + 3}}\end{align}\)

We see that upon substitution of x = 1, both the numerator and denominator become 0.

Hence, (x – 1) is a factor of both the numerator and denominator (Factor theorem)

Factorization leads to

(C) RATIONALIZATION

In this method, the rationalization of an indeterminate expression leads to determinate one. The following examples elaborate this method.

(i)  \(\mathop {\lim }\limits_{x \to 0} \frac{{\sqrt {{x^2} + 1} - 1}}{{\sqrt {{x^2} + 16} - 4}}\,\,\left( {{\rm{of\; the\;indeterminate\;form }}\frac{{\rm{0}}}{{\rm{0}}}} \right)\)

\(\begin{align}{\rm\bf{(ii)}} \quad \mathop {\lim }\limits_{x \to \infty } &\left( {\sqrt {{x^2} + x + 1} - \sqrt {{x^2} + 1} } \right) \left( {{\rm{\;of\;the\;indeterminate\;form\;}}\infty - \infty } \right)\\&= \mathop {\lim }\limits_{x \to \infty } \left( {\sqrt {{x^2} + x + 1} - \sqrt {{x^2} + 1} } \right) \times \frac{{\sqrt {{x^2} + x + 1} + \sqrt {{x^2} + 1} }}{{\sqrt {{x^2} + x + 1} + \sqrt {{x^2} + 1} }}\\&= \mathop {\lim }\limits_{x \to \infty } \frac{{({x^2} + x + 1) - ({x^2} + 1)}}{{\sqrt {{x^2} + x + 1} + \sqrt {{x^2} + 1} }}\\&= \mathop {\lim }\limits_{x \to \infty } \frac{x}{{\sqrt {{x^2} + x + 1} + \sqrt {{x^2} + 1} }}\end{align}\)

Rationalization has led us to another indeterminate form of \(\frac{\infty }{\infty }\) . However, it can easily be made determinate in the following manner:

\[\mathop {\lim }\limits_{x \to \infty } \frac{x}{{\sqrt {{x^2} + x + 1} + \sqrt {{x^2} + 1} }}\]

Now, as \(x \to \infty ,\frac{1}{x} \to 0\) and \(\frac{1}{{{x^2}}} \to 0\)

Hence, the limit above reduces to

\[\frac{1}{{\sqrt {1 + 0 + 0} + \sqrt {1 + 0} }} = \frac{1}{2}\]

(D) REDUCTION TO STANDARD FORMS

In this method, we try to reduce the given limit to one of the standard forms we studied earlier.

(i) \(\mathop {\lim }\limits_{x \to 0} {\left( {1 + \sin x} \right)^{2\cot x}}\)

This limit is of the indeterminate form \({1^\infty }\) . \(\left( {{\rm{as}}\,x \to 0,\,\,\sin x \to 0\,\,{\rm{and}}\,\,\cot x \to \infty } \right)\)

We proceed as follows:

\( = {e^{\mathop {\lim }\limits_{x \to 0} 2\cos x}} = {e^2}(\cos x \to 1\,\,\,{\rm{as}}\,\,\,x \to 0)\)

(ii) \(\begin{align}\mathop {\lim }\limits_{x \to \frac{\pi }{2}} \frac{{\cot x - \cos x}}{{{{(\pi - 2x)}^3}}}\end{align}\)

This limit is of the indeterminate form \(\frac{0}{0}\)

Let \(x = \frac{\pi }{2} + h\) so that as \(x \to \frac{\pi }{2},\,\,h \to 0.\)

\[\begin{align}\mathop {\lim }\limits_{x \to \frac{\pi }{2}} \frac{{\cot x - \cos x}}{{{{(\pi - 2x)}^3}}} &= \mathop {\lim }\limits_{h \to 0} \frac{{\cot \left( {\frac{\pi }{2} + h} \right) - \cos \left( {\frac{\pi }{2} + h} \right)}}{{{{( - 2h)}^3}}}\\
& = \mathop {\lim }\limits_{h \to 0} \left( {\frac{{ - \tan \,h + \sin \,h}}{{ - 8{h^3}}}} \right)\\
 &= \frac{1}{8}\,\,\,\mathop {\lim }\limits_{h \to 0} \,\,\frac{{ - \sin \,h + \frac{{\sin \,h}}{{\cos \,h}}}}{{{h^3}}}\
\frac{1}{8}\,\,\,\mathop {\lim }\limits_{h \to 0} \,\,\frac{{\sin \,h}}{h}.\frac{{1 - \cos \,h}}{{{h^2}}}.\frac{1}{{\cos \,h}}\\
&= \frac{1}{8}\,\,\,\mathop {\lim }\limits_{h \to 0} \,\,\frac{{\sin \,h}}{h}\,\,.\,\,\frac{{2{{\sin }^2}h/2}}{{4{{\left( {h/2} \right)}^2}}}\,\,.\,\,\frac{1}{{\cos \,h}}\\
&= \frac{1}{{16}}\,\,\,\mathop {\lim }\limits_{h \to 0} \,\,\frac{{\sin \,h}}{h}\,\,.\,\,{\left( {\frac{{\sin\;h /2}}{{\left( {h/2} \right)}}} \right)^2}\,.\,\,\frac{1}{{\cos \,h}} \end{align}\]

This expression now only contains the limits \(\mathop {\lim }\limits_{x \to 0} \frac{{\sin x}}{x} = 1\) and \(\mathop {\lim }\limits_{x \to 0} \cos x = 1\)

Hence, the final result is \(\frac{1}{{16}}\)

We will now see examples based on the methods discussed above. We urge you to first try out all  these examples on your own before viewing the solutions.