Three Dimensional Section Formula

SECTION FORMULA

Consider two arbitrary points   \(A({x_1},\,{y_1},\,{z_1})\)   and  \(B({x_2},\,{y_2},\,{z_2})\)   We need to find the coordinates of the points P and Q dividing AB internally and externally respectively, in the ratio m : n.

The approach used in the evaluation of the coordinates of P and Q is analogous to how we derived the section formula in the two dimensional case.

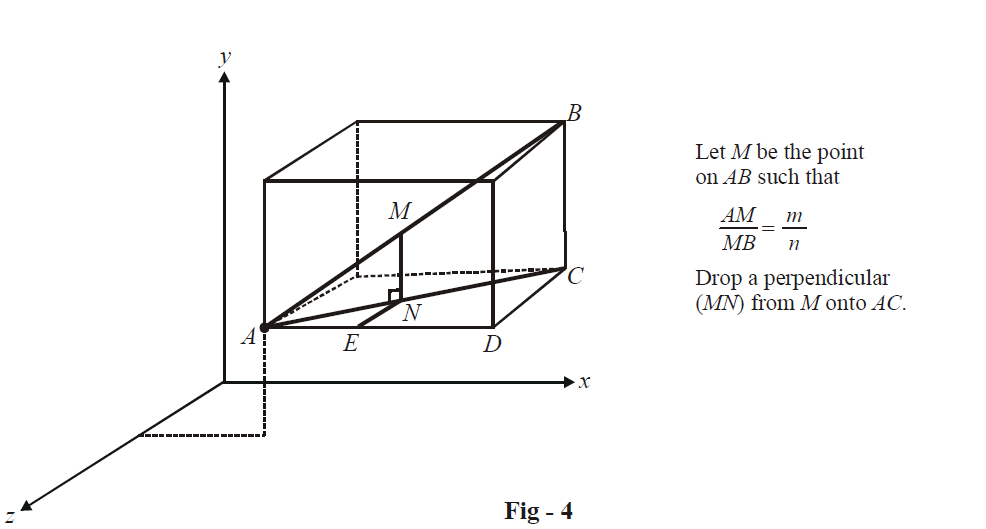
In  \(\Delta ABC,\)  we have

\[\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \ldots \left( 1 \right)\]

Assume the coordinates of M to be (x, y, z). Thus, the relation in (1) can be written as

\[\begin{align}&\qquad\;\;\frac{m}{{m + n}} = \frac{{AE}}{{AD}} = \frac{{MN}}{{BC}} = \frac{{NE}}{{CD}}\,\,\,\,\,\,\qquad\qquad\left( {\because \,\,\,\,\,{\text{in }}\Delta ACD,\,\,\frac{{AN}}{{AC}} = \frac{{AE}}{{AD}} = \frac{{NE}}{{CD}}} \right) \\\\  &\Rightarrow \quad \frac{m}{{m + n}} = \frac{{x - {x_1}}}{{{x_2} - {x_1}}} = \frac{{y - {y_1}}}{{{y_2} - {y_1}}} = \frac{{z - {z_1}}}{{{z_2} - {z_1}}} \\\\  &\Rightarrow \quad x = \frac{{m{x_2} + n{x_1}}}{{m + n}},\,\,\,y = \frac{{m{y_2} + n{y_1}}}{{m + n}},\,\,\,z = \frac{{m{z_2} + n{z_1}}}{{m + n}} \\ \end{align} \]

Thus, the coordinates of M are

\[\boxed{M \equiv \left( {\frac{{m{x_2} + n{x_1}}}{{m + n}},\,\,\,\frac{{m{y_2} + n{y_1}}}{{m + n}},\,\,\,\frac{{m{z_2} + n{z_1}}}{{m + n}}} \right)}\]

The form of the coordinates is the same as in the two dimensional case, as might have been expected. The coordinates of M ' which divides AB externally in the ratio m : n can be obtained by substituting –n for n in the coordinates of M.

As elementary applications of the section formula, do the following problems :

(a) The mid-points of the sides of a triangle are (1, 5, –1), (0, 4, –2) and (2, 3, 4). Find its vertices.

(b) Find the coordinates of the centroid of the triangle with vertices  \(\left( {{x_i},{y_i},{z_i}} \right),\,i = 1,2,3.\)