Given sin x = 3/5 and x is in quadrant 2. What is the value of tan x/2

Solution:

If x is in the quadrant 2 then x/2 is in the quadrant 1

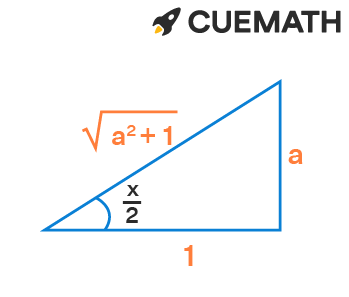
Assume the right triangle provided below

tan x/2 = a

So we get

sin (x/2) = opposite/ hypotenuse = a/√(a² + 1)

cos (x/2) = adjacent/ hypotenuse = 1/√(a² + 1)

By using the trigonometric identity 

sin 2a = 2 sin a cos a

We get

2sin (x/2) cos (x/2) = sin x

Substituting the values

2 × a/√(a² + 1) × 1/√(a² + 1) = 3/5

2 × a/a² + 1 = 3/5

By cross multiplication

10a = 3a² + 3

3a² - 10a + 3 = 0

Splitting the middle term

3a² - 9a - a + 3 = 0

3a(a - 3) - 1(a - 3) = 0

Taking out the common terms

(3a - 1)(a - 3) = 0

So we get

3a - 1 = 0 and a - 3 = 0

3a = 1 and a = 3

a = 1/3 and a = 3

So tan (x/2) = 1/3 or tan (x/2) = 3

As it lies in the Quadrant 2, tan (x/2) = 3

Therefore, the value of tan (x/2) = 3.

---

Given sin x = 3/5 and x is in quadrant 2. What is the value of tan x/2

Summary:

Given sin x = 3/5 and x is in quadrant 2. The value of tan (x/2) = 3.