Definite Integral Formula
Integration is a very important part of calculus, and in this section, we will be learning about the definite integral formula. The definite integral formula is applicable to the given upper and lower limits. The definite integral is also known as a Riemann integral If x is restricted to lie on the real line.
What is Definite Integral Formula?
The definite integral is defined as an integral with the upper and lower limits. Let's jump to the main section and go through the definite integral formulas one by one. Definite integral formula:
\(\int_a^\infty {f( x )dx} = \lim _{b \to \infty } [ {\int_a^b {f( x )dx} } ]\)
or,
\(\int_a^b {f( x )dx} = F( b ) - F( a )\)

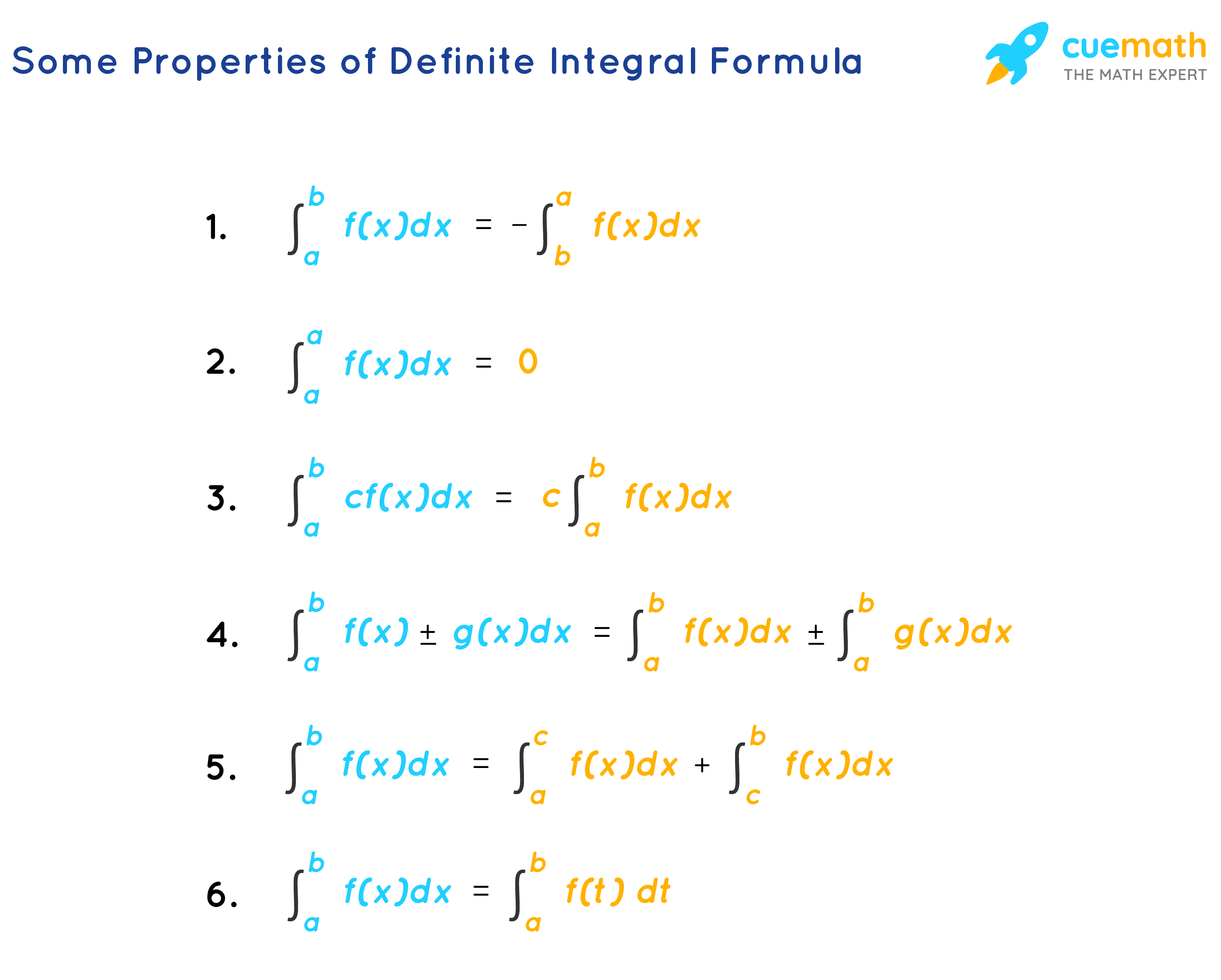
Some Properties of Definite Integral Formula:
Definite Integrals for Rational or Irrational Expression:

Solved Examples Using Definite Integral Formula
-
Example 1: Calculate the definite integral \(\int_1^2 {x^3 dx} \).
Solution:\( \int_1^2 {x^3 dx} = \left. {\frac{1}{{3 + 1}}x^{3 + 1} } \right|_1^2 = \left. {\frac{1}{4}x^4 } \right|_1^2 = \frac{1}{4}2^4 - \frac{1}{4}1^4
= \frac{1}{4} \times 16 - \frac{1}{4} \times 1 = 4 - \frac{1}{4} = \frac{{15}}{4} \)Answer: Thus, \(\int_1^2 {x^3 dx} = \frac{{15}}{4} \)
-
Example 2: Calculate the definite integral \(\int_{ - 4}^{ - 2} {6x^2 dx} \).
Solution:
\(\int_{ - 4}^{ - 2} {6x^2 dx} = {\frac{6}{{2 + 1}}x^{2 + 1} }|_{ - 4}^{ - 2} = {\frac{6}{3}x^3 }|_{ - 4}^{ - 2} = {2x^3 } |_{ - 4}^{ - 2} = 2 \times ( { - 2} )^3 - 2 \times ( { - 4} )^3 = {- 16} + 128 = 112\)Answer: Thus, \(\int_{ - 4}^{ - 2} {6x^2 dx} = 112\)
visual curriculum