A day full of math games & activities. Find one near you.
A day full of math games & activities. Find one near you.
A day full of math games & activities. Find one near you.
A day full of math games & activities. Find one near you.

Inverse Tangent Formula

The inverse tangent formula helps in connecting the various functions under inverse tangent. Here it lists the inverse tangent functions for complementary functions, inverse functions, sum and difference of functions, double of a function, and triple of a function. The inverse tangent formula helps to algebraically work across different tangent functions.

What is Inverse Tangent Formula?

The list of formulas involving inverse tangent formulas is for a single inverse tangent function for working across negative variables, and inverse of a variable. Also, these formulas include the sum and difference of two inverse tangent functions.

  • \( \text{Tan }^{-1}(-x) = -\text{Tan }^{-1}(x) \)

  • \( \text{Tan }^{-1}(x) = \text{Cot }^{-1}\dfrac{1}{x} \)

  • \( \text{Tan }^{-1}(x) + \text{Cot }^{-1}(x) = \dfrac{\pi}{2} \)

  • \(Tan ^{-1}x + Tan ^{-1}y = Tan ^{-1}\left(\dfrac{x + y}{1 - xy}\right)\)

  • \(Tan ^{-1}x - Tan ^{-1}y = Tan ^{-1}\left(\dfrac{x - y}{1 + xy}\right)\)

  • \(2Tan ^{-1}x = Tan ^{-1}\left(\dfrac{2x}{1 - x^2}\right)\)

  • \( 3Tan^{-1}x = Tan^{-1}\left(\frac{3x - x^3 }{1 - 3x^2}\right)\)

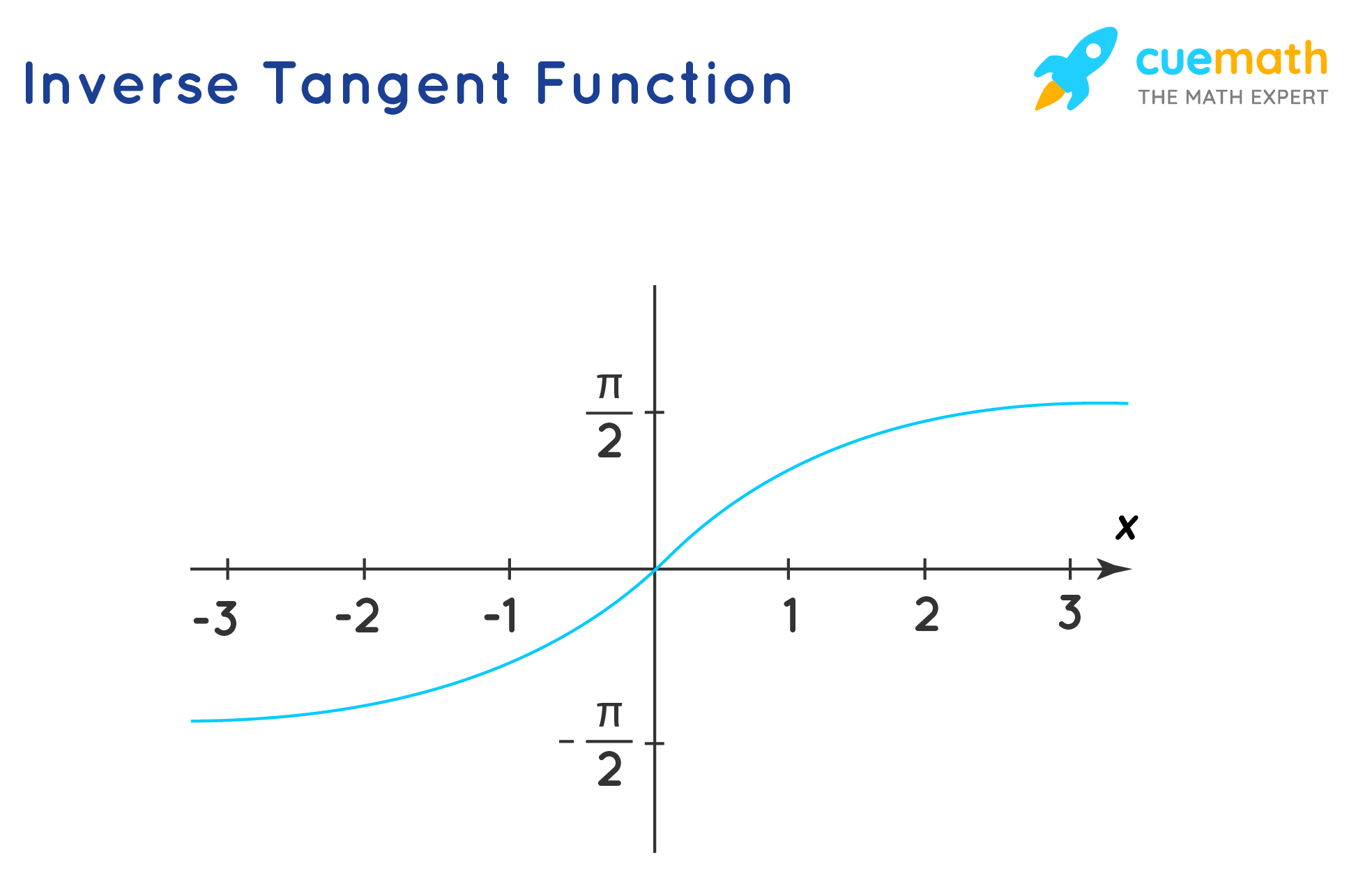
Inverse Tangent Function

Breakdown tough concepts through simple visuals.
Math will no longer be a tough subject, especially when you understand the concepts through visualizations.

Book a Free Trial Class

Let us try out the below examples to explore the use of inverse tangent formula.

Examples Using Inverse Tangent Formula

Example 1: Simplify \(Tan^{-1}(\frac{1 + Cosx}{Sinx}) \).

Solution:

\(\begin{align}Tan^{-1}(\frac{1 + Cosx}{Sinx}) &=Tan^{-1}(\frac{2Cos^2\frac{x}{2}}{2Sin\frac{x}{2}.Cos\frac{x}{2}}) \\&=Tan^{-1}(\frac{Cos\frac{x}{2}}{Sin\frac{x}{2}}) \\&=Tan^{-1}Cot\frac{x}{2} \\&=Tan^{-1}Tan(\frac{\pi}{2} - \frac{x}{2}) \\&=\frac{\pi}{2} - \frac{x}{2}\end{align}\)

Example 2: Given \(Tan^{-1}\frac{1}{2} + Tan^{-1}\frac{2}{3} = Tan^{-1}x \). Find the value of x.

Solution:

\(\begin{align}Tan^{-1}\frac{1}{2} + Tan^{-1}\frac{2}{3} &= Tan^{-1}x \\Tan^{-1}(\frac{\frac{1}{2} + \frac{2}{3}}{1 -\frac{1}{2} . \frac{2}{3}} ) &= Tan^{-1}x \\Tan^{-1}(\frac{\frac{7}{6}}{\frac{2}{3}})&=Tan^{-1}x\\Tan^{-1}(\frac{7}{6}×\frac{3}{2}) &=Tan^{-1}x \\Tan^{-1}\frac{7}{4} &=Tan^{-1}x\end{align}\)

Therefore, \(x = \frac{7}{4}\).

Math worksheets and
visual curriculum