visual curriculum
Table of Contents
| 1. | Introduction |
| 2. | Domain and Range of absolute value function |
| 3. | How to find domain and range of an absolute value function from Graphs |
| 4. | Absolute value examples |
| 5. | Summary |
| 6. | FAQs |
13 October 2020
Read time: 5 minutes
Introduction
If you’re in the mood to watch a scary movie, you may want to check out one of the five most popular horror movies of all time—I am Legend, Hannibal, The Ring, The Grudge, and The Conjuring. ( below Figure) shows the amount, in dollars, each of those movies grossed when they were released as well as the ticket sales for horror movies in general by year. Notice that we will use the data to make a function of the amount each movie earned or the total ticket sales for all horror movies by year. In creating various functions using the information, we can identify different independent and dependent variables, and we can analyze the data and the functions to determine the domain and range. In this section, we will investigate methods for determining the domain and range of absolute functions such as these.

Domain and Range of absolute value function
In Functions and Function Notation, we were introduced to the concepts of domain and range. In determining domains and ranges, we would like to think about what is physically possible or meaningful in real-world examples, like ticket sales and year in the horror movie example above. We also got to consider what is mathematically permitted. For instance, we cannot include any input value that requires us to take an even root of a negative number if the domain and range contain real numbers. Or in a function expressed as a formula, we cannot include any input value in the domain that might lead us to divide by 0.
We can visualize the domain as a “holding area” that contains “raw materials” for a “function machine” and therefore the range as another “holding area” for the machine’s products. See (Figure).

We can write the domain and range in interval notation, which uses values within brackets to explain a set of numbers. In interval notation, we use a bracket [ when the set includes the endpoint and a parenthesis ( to indicate that the endpoint is either not included or the interval is unbounded. For instance, if an individual has 100 to spend, he or she would wish to express the interval that is more than 0 and less than or equal to 100 and write \((0,100].\)
Let’s turn our attention to finding the domain of absolute value whose equation is provided. Oftentimes, finding the domain of absolute value functions involves remembering three different forms.
- First, if the absolute function has no denominator or even root, consider whether the domain of absolute value function might be all real numbers.
- Second, if there is a denominator within the absolute function’s equation, exclude values in the domain that force the denominator to be zero.
- Third, if there is even root, consider excluding values that might make the radicand negative.
Before we start, let us review the conventions of interval notation:
- The smallest number from the interval is written first.
- The largest number in the interval is written second, following a comma.
- Parentheses, ( or ), are used to indicate that an endpoint value is not included, called exclusive.
- Brackets, [ or ], are used to signify that an endpoint value is included, called inclusive.
How to find domain and range of an absolute value function from Graphs
Another way to spot the domain and range of absolute functions is by using graphs. As the domain of absolute value refers to the set of all possible input values, the domain of a graph consists of all the input values shown on the x-axis. The range of absolute value is the set of possible output values, which are shown on the y-axis. We can keep in mind that if the graph continues beyond the portion of the graph we can see, the domain and range could also be greater than the visible values. See (Figure).
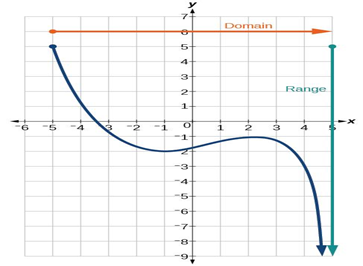
We can observe that the graph extends horizontally from \(-5\) to the right without bound, so the domain is \(\left[-5,\infty\right]\). The vertical extent of the graph is all range values \(\left[-\infty,5\right]\) and below, therefore the range of absolute value equation is 5 Note that the domain and range are always written from smaller to larger values, or from left to right for domain, and from the bottom of the graph to the top of the graph for range.
Find the domain and range of the absolute function \(f\) whose graph is shown in (Figure).

We can find that the horizontal extent of the graph is –3 to 1, so the domain of \(f\) is (-3,1]
The vertical extent of the graph is 0 to –4, so the range is \([-4,0)\) See (Figure).

Domain and Range of Absolute Value from a Graph of Oil Production
Find the domain and range of absolute function f whose graph is shown in (Figure).
(credit: modification of work by the U.S. Energy Information Administration)2

The input quantity along the horizontal axis is “years,” which we represent with the variable for time. The output quantity is “thousands of barrels of oil per day,” which we represent with the variable for barrels. The graph still to the left and right beyond what is viewed, but based on the portion of the graph that is visible, we can determine the domain and the range \(1973\le t\le2008\) as approximately \(180\le b\le2010\)
In interval notation, the domain is [1973, 2008], and the range is about [180, 2010]. For the domain and the range, we approximate the smallest and largest values since they do not fall exactly on the grid lines.
Absolute value examples
| Example 1 |
Domain and range of absolute value?
\(f(x) = |x - 3|\)
Solution :
Domain of absolute value function
A set of all defined values of x is known as domain.
Range of absolute value function
The outcomes or values that we get for y is known as the range of absolute value.Now, the domain for given absolute value function \(f(x) = |x - 3| \). For any real values of x, f(x) will give defined values. Hence the domain of absolute value is R.
Since we have absolute signs, we must get only positive values by applying any positive and negative values for x in the given function.
So, the range of absolute of absolute value is \([0, ∞).\)
| Example 2 |
Domain and range of absolute value?
\(f(x) = 1 - |x - 2|\)
Solution :
For any values of x, the function will give defined values. It will never become undefined.
So, domain of absolute value is all real values that are R.
The range of absolute value |x - 2| comes between 0 to ∞. But we want to find the range of 1 - |x - 2|
\(0 ≤ |x - 2| ≤ ∞\)
Multiplying by negative throughout the absolute value inequality, we get
\(- ∞ ≤ -|x - 2| ≤ 0\)
Add 1-, throughout the absolute value inequality, we get
\(1 - ∞ ≤ -|x - 2| ≤ 1 - 0\)
\(- ∞ ≤ -|x - 2| ≤ 1\)
So, the range of absolute value function is \((- ∞, 1].\)
| Example 3 |
Domain and range of absolute value?
\(f(x) = |x - 4|/(x - 4)\)
Solution :
\(x - 4 = 0\)
\(x = 4\)
Domain of absolute value is R - {0}
In order to find range of absolute value, we may split the given function as two parts.
\(f(x) = (x - 4)/(x - 4)\)
\(f(x) = 1 if x > 4\)
Summary
Finding the domain of absolute value functions involves remembering three different forms.
- First, if the absolute function has no denominator or even root, consider whether the domain of absolute value function might be all real numbers.
- Second, if there is a denominator within the absolute function’s equation, exclude values in the domain that force the denominator to be zero.
- Third, if there is even root, consider excluding values that might make the radicand negative.
Accordingly finding the range of absolute function.
Domain and Range can also be found using graphs.
Written by Gargi Shrivastava
Frequently Asked Questions (FAQs)
Which describes the range of the parent absolute value function?
The domain is all real numbers therefore the range is all positive numbers. The absolute parent function is \(f(x)=|x|.\) The domain, or values of x, can be any real number. There is no x that will not give an answer in this function. The range, or values of y, must be negative numbers.