Surface Area of an Equilateral Prism

The surface area of an equilateral triangular prism is the total area of all of the sides and faces of an equilateral triangular prism. In this mini topic, we will learn about the surface area of an equilateral triangle, before that, let us discuss some important pre-requisites. A prism is a solid object which has identical ends, flat faces, and the same cross-section all along its length. An equilateral triangular prism is a prism that has two parallel and congruent equilateral triangular faces and three rectangular faces perpendicular to the triangular faces.

The surface area of the equilateral triangular prism is the sum of the areas of all of the faces or surfaces of that enclosed solid. An equilateral triangular prism has three rectangular sides and two equilateral triangular faces. Thus, the surface area of an equilateral triangular prism is calculated by adding up the area of all rectangular and triangular faces. The surface area of an equilateral triangular prism can be of two types,

• Lateral surface area of equilateral triangular prism
• Total surface area of equilateral triangular prism

Let us understand the formulas to calculate LSA and TSA of equilateral triangular prism in the next section.

The formula for the surface area of an equilateral triangular prism is calculated by adding up the area of all rectangular and triangular faces of a prism. The formulas for LSA and TSA are given as:

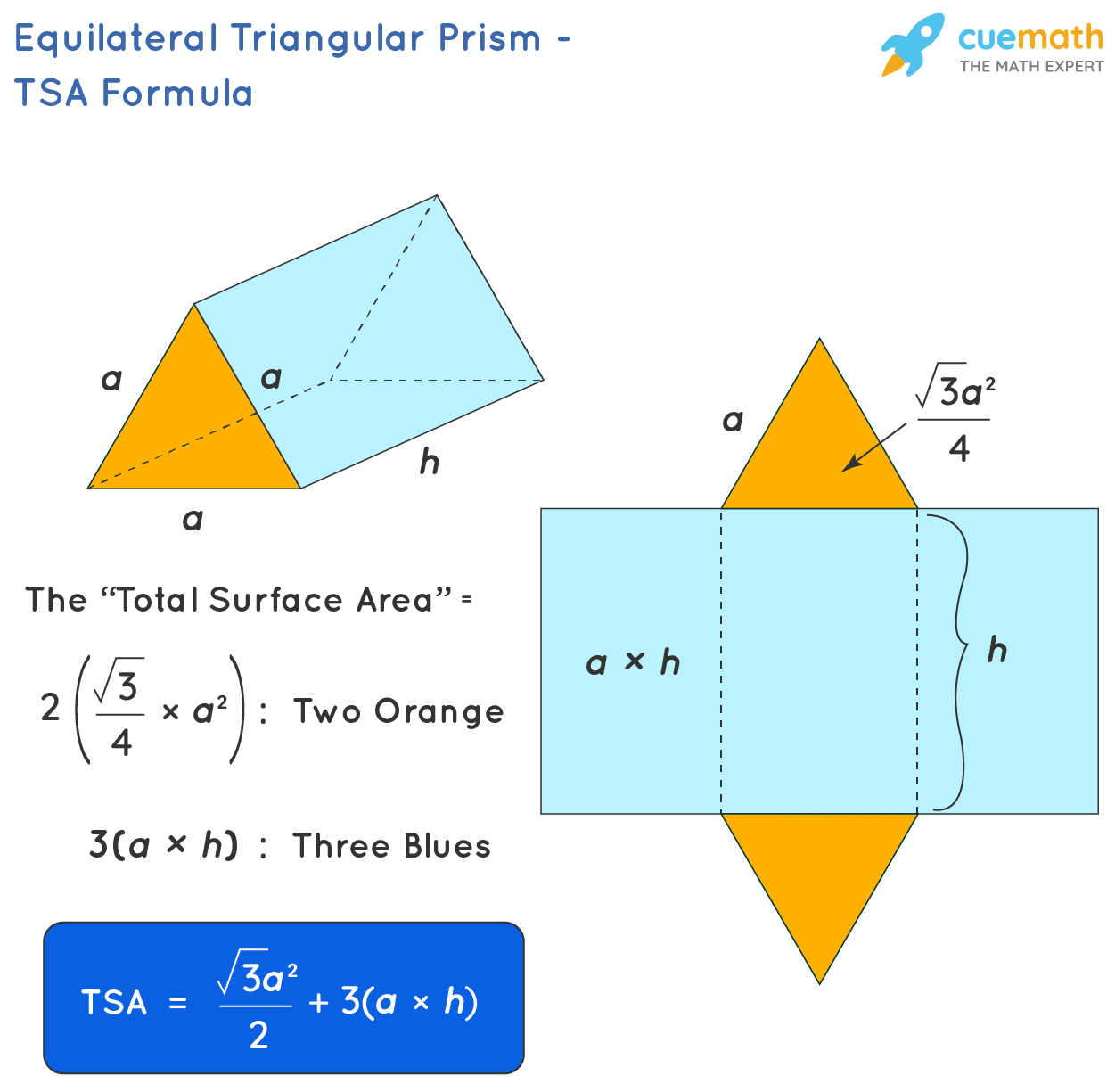
Total Surface Area of an Equilateral Triangular Prism

When 'a' is the side length of the equilateral triangle and 'h' is the height of the equilateral triangular prism, the surface area of the three rectangular faces is 3(a × h) whereas the total area of the two equilateral triangular faces is 2 × (√3a²/4). Thus,
Total surface area of an equilateral prism = (√3a²/2) + 3(a × h)
where,

• 'a' = Side length of the equilateral triangle
• 'h' = Height of the equilateral triangular prism

Lateral Surface Area of an Equilateral Triangular Prism

The lateral surface area of any object is calculated by removing the base area or the lateral surface area is the area of the non-base faces only. The lateral surface area of an equilateral triangular prism can be calculated by adding the areas of the three rectangular faces. Thus,
Lateral surface area of an equilateral triangular prism = 3(a × h)
where,

• h = Height of a prism
• a = Side length of the triangular base

The surface area of an equilateral triangular prism can be calculated by representing the 3-d figure into a 2-d net, to make the shapes easier to see. After expanding the 3-d figure into 2-d we will get two equilateral triangles and three rectangles. The following steps are used to calculate the surface area of an equilateral triangular prism :

• Calculate the area of the top and base equilateral triangles: The area of the top and base equilateral triangles is 2 × (√3a²/4).
• Calculate the area of the rectangular faces: The area of the three rectangular side faces is the height of the prism × side1, the height of the prism × side2, and the height of the prism × side 3
• Since all the sides of an equilateral triangle are the same the area of the three rectangular side faces is 3(height of the prism × any side length)
• Thus, total surface area of an equilateral triangular prism is (√3a²/2) + 3(a × h); Lateral surface area of an equilateral triangular prism = 3(a × h), where, 'h' is height of a prism and 'a' is side length of the triangular base

What Is Meant By the Surface Area of an Equilateral Triangular Prism?

The surface area of an equilateral triangular prism is defined as the area or region covered by all the faces of an equilateral triangular prism. It is expressed in square units.

How Do You Find the Area of the Base of an Equilateral Triangular Prism?

The formula for the surface area of an equilateral triangular prism is calculated by adding up the area of all rectangular and triangular faces of a prism, which is = (√3a²/2) + 3(a × h)

What Is the Formula for the Volume and Surface Area of a Triangular Prism?

The volume of a triangular prism can be found by multiplying the base times the height i.e., 1/2 × height of a base triangle × length of a prism.

What Is the Lateral Surface of an Equilateral Triangular Prism?

The lateral surface of an equilateral triangular prism is calculated by adding the areas of the three rectangular faces.

How Many Edges Are in an Equilateral Triangular Prism?

There are nine edges in an equilateral triangular prism.

What Is an Equilateral Triangular Prism?

An equilateral triangular prism is a prism that has two parallel and congruent equilateral triangular faces and three rectangular faces perpendicular to the triangular faces.