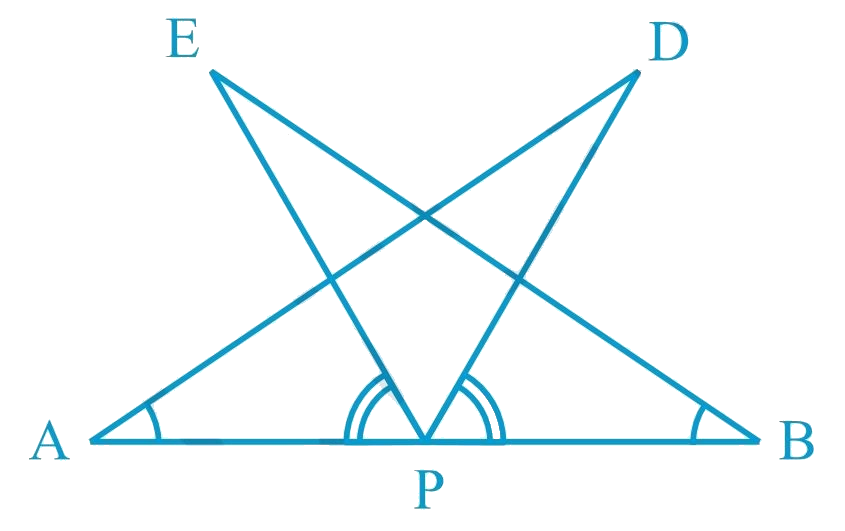
AB is a line segment and P is its mid-point. D and E are points on the same side of AB such that ∠BAD = ∠ABE and ∠EPA = ∠DPB (see Fig. 7.22). Show that i) ΔDAP ≅ ΔEBP  ii) AD = BE

Solution:

Given: P is its mid-point of AB, ∠BAD = ∠ABE and ∠EPA = ∠DPB

To Prove: i) ΔDAP ≅ ΔEBP and (ii) AD = BE.

Reasoning: We can show two triangles DAP and EBP congruent by using ASA congruency rule and then we can say corresponding parts of congruent triangles will be equal. 

i) It is given that ∠EPA = ∠DPB

∠EPA + ∠DPE = ∠DPB + ∠DPE (∠DPE is common)

∴ ∠DPA = ∠EPB

In ΔDAP and ΔEBP,

∠DAP = ∠EBP (Given)

AP = BP (P is mid - point of AB)

∠DPA = ∠EPB (Proven above)

∴ ΔDAP ≅ ΔEBP (ASA congruence rule)

ii) Since, ΔDAP ≅ ΔEBP 

∴ AD = BE (By CPCT)

☛ Check: NCERT Solutions Class 9 Maths Chapter 7

Video Solution:

AB is a line segment and P is its mid-point. D and E are points on the same side of AB such that. ∠BAD = ∠ABE and ∠EPA = ∠DPB (see Fig. 7.22). Show that
i) ΔDAP ≅ ΔEBP
ii) AD = BE

NCERT Maths Solutions Class 9 Chapter 7 Exercise 7.1 Question 7

Summary:

If AB is a line segment and P is its mid-point, D and E are points on the same side of AB such that ∠BAD = ∠ABE and ∠EPA  = ∠DPB, then ΔDAP ≅ ΔEBP using AAS congruence and AD = BE by CPCT.

☛ Related Questions:

• AD and BC are equal perpendiculars to a line segment AB (See the given figure). Show that CD bisects AB.
• l and m are two parallel lines intersected by another pair of parallel lines p and q. Show that ΔABC ≅ ΔCDA.
• Line l is the bisector of an angle ∠A and B is any point on l. BP and BQ are perpendiculars from B to the arms of ∠A (see the given figure). Show that:i) ΔAPB ≅ ΔAQBii) BP = BQ or B is equidistant from the arms of ∠A
• In the given figure, AC = AE, AB = AD and ∠BAD = ∠EAC. Show that BC = DE.