Congruence in Triangles
Congruence in two or more triangles depends on the measurements of their sides and angles. The three sides of a triangle determine its size and the three angles of a triangle determine its shape. Two triangles are said to be congruent if pairs of their corresponding sides and their corresponding angles are equal. They are of the same shape and size. There are many conditions of congruence in triangles. Let us discuss them in detail.
| 1. | Congruence in Triangles |
| 2. | Conditions of Congruence in Triangles |
| 3. | Solved Examples |
| 4. | Practice Questions |
| 5. | FAQs on Congruence in Triangles |
What is Congruence in Triangles?
If the three angles and the three sides of a triangle are respectively equal to the corresponding angles and the corresponding sides of another triangle, then both the triangles are said to be congruent. In the Δ PQR and ΔXYZ, as shown below, we can identify that PQ = XY, PR = XZ, and QR = YZ and ∠P = ∠X, ∠Q = ∠Y and ∠R = ∠Z. Then we can say that Δ PQR ≅ ΔXYZ.
The two triangles need to be of the same size and shape to be congruent. Both the triangles under consideration should superimpose on each other. When we rotate, reflect, and/ or translate a triangle, its position or appearance seems to be different. In that case, we need to identify the six parts of a triangle and their corresponding parts in the other triangle. Consider Δ ABC and ΔPQR as shown below.
| Corresponding Vertices | A and P, B and Q, C and R |
|---|---|
| Corresponding Sides | AB = PQ, BC = QR, CA = RP |
| Corresponding Angles | ∠A = ∠P, ∠B = ∠Q and ∠C = ∠R |
Thus on identifying the corresponding parts of the given triangles, we can confirm that Δ ABC ≅ ΔPQR.
Conditions of Congruence in Triangles
Two triangles are said to be congruent if they are of the same size and same shape. Necessarily, not all the six corresponding elements of both the triangles must be found to be equal to determine that they are congruent. Based on studies and experiments, there are 5 conditions for two triangles to be congruent. They are SSS, SAS, ASA, AAS, and RHS congruence properties.
SSS Criterion for Congruence
SSS Criterion stands for Side-Side-Side Criterion. Under this criterion, two triangles are congruent if three sides of a triangle are equal to the corresponding sides of the other triangle.
If Δ BAC ≅ ΔXYZ under SSS criterion, then the three angles of ΔBAC are bound to be equal to the corresponding angles of ΔXYZ.
SAS Criterion for Congruence
SAS Criterion stands for Side-Angle-Side Criterion. Under this criterion, two triangles are congruent if the two sides and the included angle of one triangle are equal to the corresponding sides and the included angle of the other triangle.
If Δ ABC ≅ ΔXYZ under SAS criterion, then the third side (AB) and the other two angles of Δ ABC are bound to be equal to the corresponding side (XY) and the angles of ΔXYZ.
ASA Criterion for Congruence
ASA Criterion stands for Angle-Side-Angle Criterion. Under ASA criterion, two triangles are congruent if any two angles and the side included between them of one triangle are equal to the corresponding angles and the included side of the other triangle.
If Δ ABC ≅ ΔXYZ under ASA criterion, then the third angle (∠BAC) and the other two sides of Δ ABC are bound to be equal to the corresponding angle (∠YXZ) and the sides of ΔXYZ.
AAS Criterion for Congruence
AAS Criterion stands for Angle-Angle-Side Criterion. Under the AAS criterion, two triangles are congruent if any two angles and the non-included side of one triangle are equal to the corresponding angles and the non-included side of the other triangle.
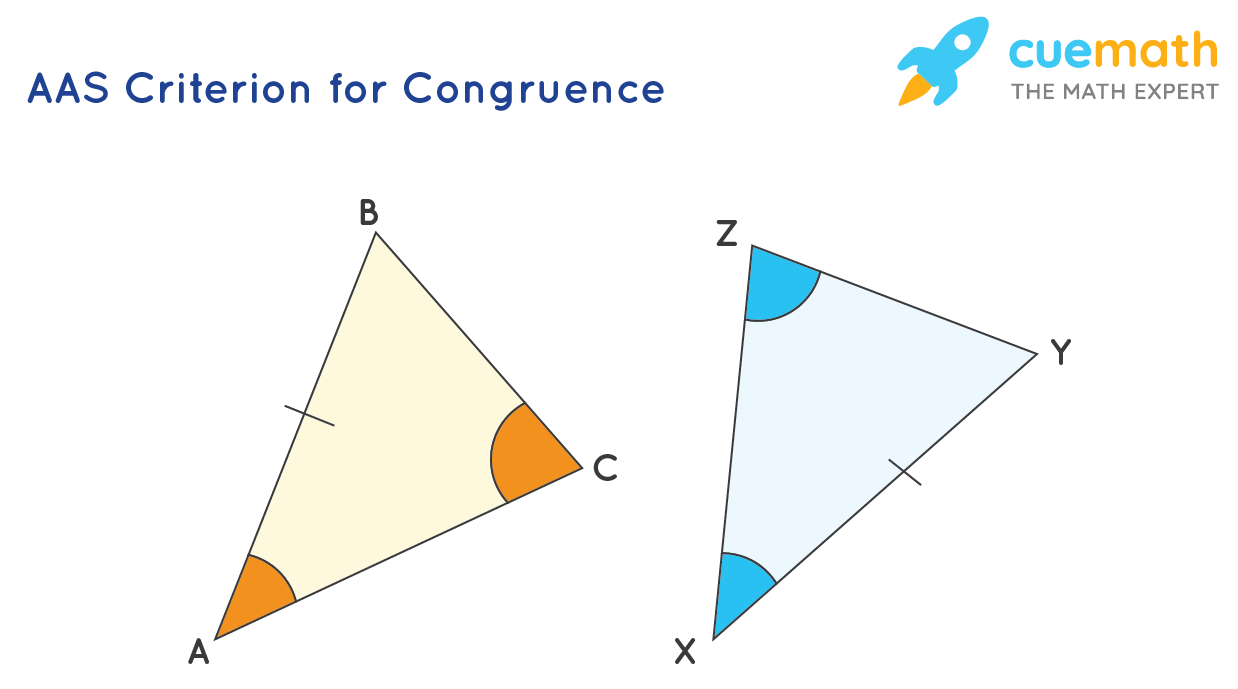
If Δ ABC ≅ ΔXYZ under AAS criterion, then the third angle (∠ABC) and the other two sides (AC and BC) of Δ ABC are bound to be equal to the corresponding angle (∠XYZ) and the sides (XZ and YZ) of ΔXYZ.
RHS Criterion for Congruence
RHS criterion stands for right angle-hypotenuse-side congruence criterion. Under this criterion, two triangles are congruent, if the hypotenuse and side of one right-angled triangle are equal to the hypotenuse and the corresponding side of another right-angled triangle.
If Δ ABC ≅ ΔXYZ under RHS criterion, then the third side (AB) and the other two angles of Δ ABC are bound to be equal to the corresponding side (XY) and angles of ΔXYZ.
Important notes
- Two triangles are congruent if the six parts of one triangle are equal to the corresponding six parts of the other triangle.
- There are five conditions to determine if two triangles are congruent. They are SSS, SAS, ASA, AAS, and RHS criteria.
- Two triangles with equal corresponding angles may not be congruent to each other because one triangle might be an enlarged copy of the other. Hence, there is no AAA Criterion for Congruence.
- We represent the congruency by using the symbol (≅).
- If two triangles are congruent then their perimeters and areas are equal.
Congruence in Triangles Related Topics
Also, check topics related to congruence in triangles:
Congruence in Triangles Examples
-
Example 1: PQR is an isosceles triangle. L and M are the midpoints of the equal sides of the triangle. N is the midpoint of the third side. Prove that LN=MN.
Solution:
Given that Δ PQR is an isosceles triangle. L is the midpoint of PQ and M is the midpoint of QR.
To prove: LN = MN
Proof: It is enough to prove that ΔLPN ≅ ΔMRN to prove that LN is equal to MN.
We conclude the following with the given and known facts:
PQ = QR (Two sides are equal in an isosceles triangle)
∠QPR = ∠PRQ (Angles opposite to equal sides are equal)
PL = LQ = QM = MR (Since L and M are midpoints of PQ and QR respectively and PQ = QR)
In ΔLPN and ΔMRN, we have
- LP = MR (Since L and M are midpoints and PQ = QR)
- ∠LPN = ∠MRN (Since ∠QPR = ∠QRP)
- PN = NR (N is the midpoint of PR)
Then by SAS criterion of congruence in triangles, ΔLPN ≅ ΔMRN. Since congruent parts of congruent triangles are equal, LN = MN. Hence proved.
-
Example 2: Check if the given triangles below are congruent and state the criterion test for congruence in triangles.
Solution:
Let us identify the corresponding parts in the triangles.
We observe that EF = MO = 3 inches
FG = ON = 4.5 inches
∠EFG = ∠MON = 110°
Thus by identifying the corresponding parts we conclude that Δ EFG ≅ Δ MON by SAS criterion.
-
Example 3: Identify the rule of congruence in the triangles ABC and DCB, and prove that they are congruent triangles.
Solution:
ln ΔABC and ΔDCB, let us try to identify any three parts of one triangle equal to the corresponding parts of the other triangle.
By observation, we find that AB = DC, AC = DB, and BC is common.
Thus by SSS rule of congruence, ΔABC ≅ ΔDCB
FAQs on Congruence in Triangles
What are Congruent Triangles?
Two triangles are said to be congruent if they are of the same size and same shape. Two congruent triangles have the same area and perimeter. All the sides and angles of a congruent triangle are equal to the corresponding sides and angles of its congruent triangle. We can prove the congruency of any two triangles by using five different properties, which are - SSS, SAS, AAS, ASA, and RHS.
What are the Tests of Congruence in Triangles?
Two triangles are congruent if they satisfy the 5 conditions of congruence. They are side-side-side(SSS), side-angle-side (SAS), angle-side-angle(ASA), angle-angle-side (AAS) and Right angle-Hypotenuse-Side(RHS).
How can you Identify the Congruence in Triangles?
If we identify the parts of one triangle equal to the corresponding parts of the other triangle, we can identify the congruence in triangles.
What are Congruent Triangles?
Two triangles are congruent if they are exact copies of each other and when superimposed they cover each other exactly. Two congruent triangles have the same perimeter and area.
What are the Properties of Congruent Triangles?
There are 5 properties of congruent triangles which form the conditions to determine if they are congruent or not. They are:
- SSS Criterion for Congruence
- SAS Criterion for Congruence
- ASA Criterion for Congruence
- AAS Criterion for Congruence
- RHS Criterion for Congruence
How to Prove Congruence in Triangles?
If two triangles are congruent then at least 3 parts of one triangle should be equal to the corresponding parts of the other triangle. We can use side-side-side(SSS), side-angle-side (SAS), angle-side-angle(ASA), angle-angle-side (AAS) and Right angle-Hypotenuse-Side(RHS) tests of congruence to prove the same.
Can we prove Congruence in Triangles using AAA criterion?
No, we cannot prove congruence in triangles using AAA criterion. If two triangles are congruent then at least 3 parts of one triangle should be equal to the corresponding parts of the other triangle. However, if 3 angles of one triangle are equal to the corresponding angles of the other triangle, there is a chance of them being similar triangles. Two equilateral triangles have all three angles equal, but their sides could be different, and hence they won't be congruent instead of having three similar angles. So, AAA is not a congruence criterion.