How to find how many standard deviations are away from the mean?
The statement signifies the magnitude of the standard deviation deferred from the mean of the data.
Answer: The value of standard deviation, away from mean is calculated by the formula, X = µ ± Zσ
The standard deviation can be considered as the average difference (positive difference) between an observation and the mean.
Explanation:
Let Z denote the amount by which the standard deviation differs from the mean.
Therefore, Z = (X - µ)/σ
where µ denotes the mean,
σ denotes the standard deviation,
X is the value of standard deviation away from the mean.
⇒ X = µ ± Zσ
Let us try to understand the above value of X using the graph given below and study at certain points.
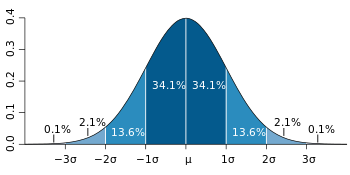
( Standard deviation away from the mean i.e center of the graph )
For example,
µ - 2σ (which shows two standard deviations below the mean)
µ - σ (which shows 1 standard deviation below the mean)
µ (which shows 0 standard deviations from the mean or exact mean)
µ + σ (which shows 1 standard deviation above the mean)