Standard Deviation
Standard deviation is the positive square root of the variance. It is one of the basic methods of statistical analysis. Standard Deviation is commonly abbreviated as SD and denoted by the symbol 'σ’ and it tells about how much data values are deviated from the mean value. If we get a low standard deviation then it means that the values tend to be close to the mean whereas a high standard deviation tells us that the values are far from the mean value.
We have separate formulas to calculate the standard deviation of grouped and ungrouped data. Also, we have different standard deviation formulas to calculate SD of a random variable. Let us look into all the formulas in detail.
What is Standard Deviation?
Standard deviation is the degree of dispersion or the scatter of the data points relative to its mean, in descriptive statistics. It tells how the values are spread across the data sample and it is the measure of the variation of the data points from the mean. The standard deviation of a data set, sample, statistical population, random variable, or probability distribution is the square root of its variance.
When we have n number of observations and the observations are \(x_1, x_2, .....x_n\), then the mean deviation of the value from the mean is determined as \(\sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2}\). However, the sum of squares of deviations from the mean doesn't seem to be a proper measure of dispersion. If the average of the squared differences from the mean is small, it indicates that the observations \(x_i\) are close to the mean \(\bar x\). This is a lower degree of dispersion. If this sum is large, it indicates that there is a higher degree of dispersion of the observations from the mean \(\bar x\). Thus we conclude that \(\sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2}\) is a reasonable indicator of the degree of dispersion or scatter.
We take \(\dfrac{1}{n}\sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2}\) as a proper measure of dispersion and this is called the variance(σ2). The positive square root of the variance is the standard deviation.
Standard Deviation Formula
The spread of statistical data is measured by the standard deviation. The degree of dispersion is computed by the method of estimating the deviation of data points. You can read about dispersion in summary statistics. As discussed, the variance of the data set is the average square distance between the mean value and each data value. And standard deviation defines the spread of data values around the mean. Here are two standard deviation formulas that are used to find the standard deviation of sample data and the standard deviation of the given population.

Note that both formulas look almost similar except for the denominator which is N in the case of the population SD but n-1 in the case of the sample SD. While calculating the sample mean, all the data values in the population are not considered so the sample mean just is an estimate of the population mean, but this introduces some uncertainty or bias in our calculation of standard deviation. To adjust this, the denominator of the sample standard deviation is corrected to be n-1 instead of just n. This is known as Bessel's correction.
Formula for Calculating Standard Deviation
There are two types of data sets: populations and samples. A population is an entire group that we are interested in studying, while a sample is a smaller group of individuals that is taken from the population. The formulas to calculate the standard deviations of population and sample differ a little.
The population standard deviation formula is given as:
\(\sigma=\sqrt{\frac{1}{N} \sum_{i=1}^{N}\left(X_{i}-\mu\right)^{2}}\)
Here,
- σ = Population standard deviation symbol
- μ = Population mean
- N = total number of observations
Similarly, the sample standard deviation formula is:
\(s=\sqrt{\frac{1}{n-1} \sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2}}\)
Here,
- s = Sample standard deviation symbol
- \(\bar x\) = Arithmetic mean of the observations
- n = total number of observations
How to Calculate Standard Deviation?
In general, the standard deviation refers to the population standard deviation and here are the steps to calculate the standard deviation of a set of data values:
- Find the mean, which is the arithmetic mean of the observations.
- Find the squared differences from the mean. (The data value - mean)2
- Find the average of the squared differences. (Variance = The sum of squared differences ÷ the number of observations)
- Find the square root of variance. (Standard deviation = √Variance)
Standard Deviation of Ungrouped Data
The calculations for standard deviation differ for different data. Distribution measures the deviation of data from its mean or average position. There are three methods to find the standard deviation.
- Actual mean method
- Assumed mean method
- Step deviation method
Standard Deviation by The Actual Mean Method
In this method, we first compute the mean of the data values (\(\bar x\)) and then compute the deviations of each data value from the mean. Then we use the following standard deviation formula by actual mean method:
σ = √(∑\((x-\bar x)\)2 /n), where n = total number of observations.
Consider the data observations 3, 2, 5, 6. Here the mean of these data points is (3 + 2 + 5 + 6)/4 = 16/4 = 4.
The sum of the squared differences from mean = (4-3)2+(2-4)2 +(5-4)2 +(6-4)2 = 10
Variance = Squared differences from mean/ number of data points =10/4 =2.5
Standard deviation = √2.5 = 1.58
Standard deviation by Assumed Mean Method
When the x values are large, an arbitrary value (A) is chosen as the mean (as the computation of mean is difficult in this case). The deviation from this assumed mean is calculated as d = x - A. Then the standard deviation formula by assumed mean method is:
σ = √[(∑(d)2 /n) - (∑d/n)2]
Standard Deviation by Step Deviation Method
The standard deviation of grouped data also can be calculated by "step deviation method". In this method also, some arbitrary data value is chosen as the assumed mean, A. Then we calculate the deviations of all data values by using d = x - A. The next step is to calculate the step deviations (d') using d' = d/i where 'i' is a common factor of all 'd' values (choose any common factor in case of multiple factors). Now, the standard deviation of ungrouped data by step deviation method is found by the formula:
σ = √[(∑(d')2 /n) - (∑d'/n)2] × i, where 'n' is the total number of data values.
Standard Deviation of Grouped Data (Discrete)
When the data points are grouped, we first construct a frequency distribution. Just like ungrouped data, the standard deviation of grouped data can also be calculated using 3 methods: actual mean method, assumed mean method, and step deviation method. Let us dive into each of these methods.
Standard Deviation of Discrete Data by Actual Mean Method
For n number of observations, \(x_1, x_2, .....x_n\), and the corresponding frequencies, \(f_1, f_2, f_3, ...f_n\) the standard deviation is:
\(\sigma=\sqrt{\frac{1}{n} \sum_{i=1}^{n}f_i \left(x_{i}-\bar x\right)^{2}}\). Here
- n = total frequency = \(\sum_{i=1}^{n}f_i\)
- \(\bar x\) = mean
Example: Let's calculate the standard deviation for the data given below:
| xi | 6 | 10 | 12 | 14 | 24 |
|---|---|---|---|---|---|
| fi | 2 | 3 | 4 | 5 | 4 |
Calculate mean(\(\bar x\)): (6 × 2 + 10 × 3 + 12 × 4 + 14 × 5 + 24 × 4)/(2+3+4+5+4) = 14.22
| xi | fi | fixi | xi - \(\bar x\) | (xi - \(\bar x\))2 | fi (xi - \(\bar x\))2 |
|---|---|---|---|---|---|
| 6 | 2 | 12 | -8.22 | 67.5684 | 135.1368 |
| 10 | 3 | 24 | -4.22 | 17.8084 | 53.4252 |
| 12 | 4 | 40 | -2.22 | 4.9284 | 19.7136 |
| 14 | 5 | 60 | -0.22 | 0.0484 | 0.242 |
| 24 | 4 | 56 | 9.78 | 95.6484 | 382.5936 |
| 18 | 192 | 591.1112 |
Now, variance: σ2 = 1/n \(\sum_{i=1}^{n}f_i \left(x_{i}-\bar x\right)^{2}\)
= 1/18 × 591.1112 = 32.83
Calculate SD: σ = √Variance = √32.83 = 5.73
Standard Deviation of Discrete Data by Assumed Mean Method
When the data values are very large, then one of the data values is chosen as the mean (and hence is known as assumed mean, A). Then the deviation of each data value from the assumed mean is d = x - A. Then the formula for standard deviation by assumed mean method is:
σ = √[(∑(fd)2 /n) - (∑fd/n)2], where
- 'f' is the frequency of corresponding data value x and
- 'n' is the total frequency.
Standard Deviation of Discrete Data by Step Deviation Method
The standard deviation of grouped data can be calculated by another method called the "step deviation method". In this method also, we assume some data value as the mean (assumed mean, A) and calculate the deviations of data values using d = x - A. In this method, we also find the step deviations (d') using d' = d/i where i = any number that is a common factor of all values represented by 'd' (there can be multiple factors, but we can choose any). Now, the standard deviation by step deviation method is calculated by the formula:
σ = √[(∑(fd')2 /n) - (∑fd'/n)2] × i, where
- 'f' is the frequency of data values
- 'n' is the total frequency
- 'i' is a common factor of all 'd' values, where d = x - A (A = assumed mean)
- d' = d/i
Standard Deviation of Grouped Data (Continuous)
If the frequency distribution is continuous, each class is replaced by its midpoint. Then the standard deviation is calculated by the same technique as in discrete frequency distribution. Consider the following example. \(x_i\) is calculated as the midpoint of each class which is calculated by the formula (lower bound + upper bound)/2. Then the same standard deviation formula is applied.
| Class | fi | xi |
|---|---|---|
| 0-10 | 3 | 5 |
| 10-20 | 4 | 15 |
| 20-30 | 6 | 25 |
| 30-40 | 4 | 35 |
| 40-50 | 8 | 40 |
Now, the standard deviation can be calculated by using the formulas of grouped data either in the actual mean method, assumed mean method, or step deviation method.
Standard Deviation of Random Variables
The measure of spread for the probability distribution of a random variable determines the degree to which the values differ from the expected value. This is a function that assigns a numerical value to each outcome in a sample space. This is denoted by X, Y, or Z, as it is a function. If X is a random variable, the standard deviation is determined by taking the square root of the sum of the product of the squared difference between the random variable, X, and the expected value (𝜇 (or) E(X)) and the probability associated value of the random variable.
The standard deviation of the probability distribution of X, 𝜎 = \(\sqrt{\Sigma\left[(x-\mu)^2 \cdot P(x)\right]}\)
The shortcut to finding the standard deviation of random variables is: 𝜎 = \(\sqrt{E(X^2)-[E(X)]^2}\) (or) 𝜎 = \(\sqrt{\Sigma\left[x^2 \cdot P(x)\right]-\mu^2}\)
Standard Deviation of Probability Distribution
The experimental probability consists of many trials. When the difference between the theoretical probability of an event and its relative frequency get closer to each other, we tend to know the average outcome. This mean is known as the expected value of the experiment denoted by 𝜇.
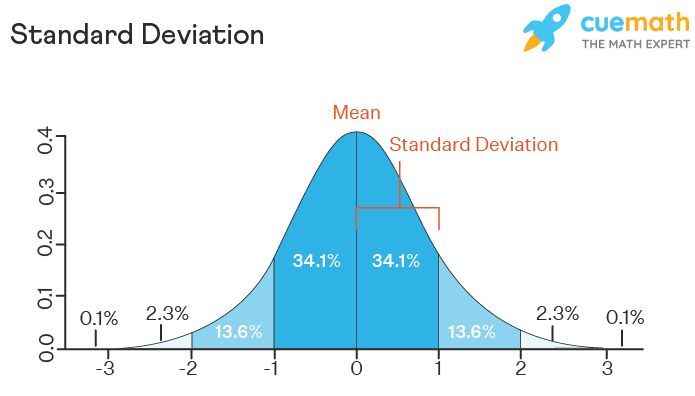
- In a normal distribution, the mean is zero and the standard deviation is 1.
- In a binomial experiment, the number of successes is a random variable. If a random variable has a binomial distribution, its standard deviation is given by: 𝜎 = √npq, where mean: 𝜇 = np, n = number of trials, p = probability of success and 1-p =q is the probability of failure.
- In a Poisson distribution, the standard deviation is given by 𝜎= √λt, where λ is the average number of successes in an interval of time t.
Important Notes on Standard Deviation:
- The square root of the average of the squared differences of data observations from the mean is called the standard deviation.
- Standard deviation is the positive square root of variance.
- Standard deviation is the indicator that shows the dispersion of the data points about the mean.
☛ Related Articles:
- Standard Deviation Calculator
- Mean and Standard Deviation Calculator
- Mean Median Standard Deviation Calculator
- Variance and Standard Deviation
Cuemath is one of the world's leading math learning platforms that offers LIVE 1-to-1 online math classes for grades K-12. Our mission is to transform the way children learn math, to help them excel in school and competitive exams. Our expert tutors conduct 2 or more live classes per week, at a pace that matches the child's learning needs.
Standard Deviation Examples
-
Example 1: There are 39 plants in the garden. A few plants were selected randomly and their heights in cm were recorded as follows: 51, 38, 79, 46, 57. Calculate the standard deviation of their heights.
Solution:
n = 5
Sample mean (\(\bar{x}\))= (51+38+79+46+57)/5 = 54.2
Since, sample data is given, we use the sample SD formula.
SD = \( \sqrt{\dfrac{\Sigma (x_i-\bar{x})^2}{n-1}} \)
= \( \sqrt{\frac{(51-54.2)^2 +(38-54.2)^2 +(79-54.2)^2 +(46-54.2)^2 +(57-54.2)^2}{4}} \)
= 15.5
Answer: Standard deviation for this data is 15.5
-
Example 2: In a class of 50, 4 students were selected at random and their total marks in the final assessments are recorded, which are: 812, 836, 982, and 769. Find the variance and standard deviation of their marks.
Solution:
n = 4
Sample Mean (X̄) = (812+836+982+769)/4 = 849.75
Here also, we have to calculate the sample standard deviation as the given data is just a sample.
Variance = \( \dfrac{\sum^{N}_{i=1} (X_i - \bar{X})^2}{n-1} \)
= \( \dfrac{\sum^{4}_{i=1} (X_i - 849.75)^2}{3} \)
= [(812 - 849.75)2 + (836 - 849.75)2 + (982 - 849.75)2 + (769 - 849.75)2] /3
= 8541.58
Using the SD formula,
SD = √8541.58 = 92.4
Answer: Variance is 8541.58 and standard deviation for this data is 92.4
-
Example 3: Find the standard deviation of X which has the probability distribution as shown in the table below.
X P(X) 4 0.2 5 0.3 6 0.5 Solution:
To find the expected value of X, find the product X. P(X) and sum these terms.
X P(X) X. P(X) 4 0.2 0.8 5 0.3 1.5 6 0.5 3.0 E(X) = 0.8+1.5+3.0
=5.3
X P(X) (X - E(X))2 (X - E(X))2. P(X) 4 0.2 1.69 0.338 5 0.3 0.09 0.027 6 0.5 0.49 0.245 Standard Deviation = √(6.76+0.45+2.94)
= √0.61 ≈ 0.78
Answer: The standard deviation of the probability distribution is 0.78

FAQs on Standard Deviation
What is the Meaning of Standard Deviation?
The standard deviation means the measure of dispersion or the spread of the data about the mean value. It helps us to compare the sets of data that have the same mean but a different range. The sample standard deviation formula is: \(s=\sqrt{\frac{1}{n-1} \sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2}}\), where \(\bar x\) is the sample mean and \(x_i\) gives the data observations and n denotes the sample size.
What are Standard Deviation Formulas for Population and Sample?
If 'n' is the number of observations and \(\bar x\) is the population/sample mean then:
- Population standard deviation formula is: \(\sigma=\sqrt{\frac{1}{n} \sum_{i=1}^{n}\left(x_{i}-\bar{x} \right)^{2}}\)
-
Sample standard deviation formula is: \(s=\sqrt{\frac{1}{n-1} \sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2}}\)
How Do You Calculate Standard Deviation?
To find the standard deviation:
- First, see whether the data values represent the population or sample.
- If they represent the sample, then use the sample standard deviation formula √ [ 1/(n-1) ∑(xi - sample mean)2.
- If they represent the population, then use the population standard deviation formula √ [ 1/n ∑(xi - population mean)2.
What are Standard Deviation Formulas for Ungrouped Data?
When the data is ungrouped, the standard deviation (SD) can be calculated in the following 3 methods. The corresponding SD formulas are:
- Actual mean method: σ = √(∑\((x-\bar x)\)2 /n)
- Assumed mean method: σ = √[(∑(d)2 /n) - (∑d/n)2]
- Step deviation method: σ = √[(∑(d')2 /n) - (∑d'/n)2] × i
For a detailed understanding of each of these methods, refer to the page above.
Give a Standard Deviation Example.
Let us find the standard deviation of the data points 1, 3, 4, 5. The mean is 13/4 = 3.25. The average of mean differences = [(3.25-1)2 + (3-3.25)2+ (4-3.25)2 + (5-3.25)2]/4 = 2.06. The standard deviation = √2.06 = 1.43.
What are Standard Deviation Formulas for Grouped Data?
Groped data can be discrete or continuous. Here are the standard deviation formulas for grouped discrete data by different methods. In case, the data is continuous, the data values will be the midpoints of the class intervals, and then the standard deviation can be calculated by the same formulas as discrete data.
- By actual mean method: σ = √(∑\(f(x-\bar x)\)2 /n)
- By assumed mean method: σ = √[(∑(fd)2 /n) - (∑fd/n)2]
- By step deviation method: σ = √[(∑(fd')2 /n) - (∑fd'/n)2] × i
To understand the process of calculating the standard deviation in detail, scroll this age up.
What Is the Difference Between Standard Deviation Formula and Variance Formula?
Variance is the average of the squared deviations from the mean, while standard deviation is the square root of this number. Both measures reflect variability in distribution, but their units differ: Standard deviation is expressed in the same units as the original values (e.g., minutes or meters). Sample standard deviation formula = √[ Σ (xi – x̅)2/(n-1) ] and variance formula = σ2 = Σ (xi – x̅)2/(n-1)
What Is Mean-Variance and Standard Deviation in Statistics?
Variance is the sum of squares of differences between all numbers and means. Standard Deviation is the square root of variance. It is a measure of the extent to which data varies from the mean. The standard deviation formula is √variance.
Which Is Better to Use Variance Formula or Standard Deviation Formula?
They each have different purposes. The SD is usually more useful to describe the variability of the data while the variance is usually much more useful mathematically. For example, the sum of uncorrelated distributions (random variables) also has a variance that is the sum of the variances of those distributions.
Why Do We Use Standard Deviation Formula and Variance?
Standard deviation looks at how spread out a group of numbers is from the mean, by looking at the square root of the variance. The variance measures the average degree to which each point differs from the mean.
visual curriculum