Normal Distribution Formula 

The normal distribution or bell curve or the gaussian distribution is the most significant continuous probability distribution in probability and statistics. In physical science and economics, a vast number of random variables of interest are either nearly or exactly described by the normal distribution. The normal distribution formula can be used to approximate other probability distributions as well.

The random variables which follow the normal distribution are ones whose values can assume any known value in a given range.

What Is Normal Distribution Formula?

The normal distribution is defined by the probability density function f(x) for the continuous random variable X considered in the system. It is a function whose integral across an interval (say x to x + dx) gives the probability of the random variable X, by considering the values between x and x + dx. Since there will be infinite values between x and x + dx, thus, a range of x is considered, and a continuous probability density function is defined as

\(\begin{array}{l}
 f\left( x \right) \ge 0 \ \forall \ x \in \left( { - \infty , + \infty } \right) \\ 
 \int_{ - \infty }^{ + \infty } {f\left( x \right) = 1}  \\ 
 \end{array}\)

For a normal distribution of a random variable X with the mean = μ and the variance = σ², the probability density f(x) is given by; :

\(f\left( x \right) = \frac{1}{{\sigma \sqrt {2\pi } }}e^{\frac{{ - \left( {x - \mu } \right)^2 }}{{2\sigma ^2 }}}\)

An equivalent representation:

\( X\sim N( {\pi ,\sigma ^2 }) \)

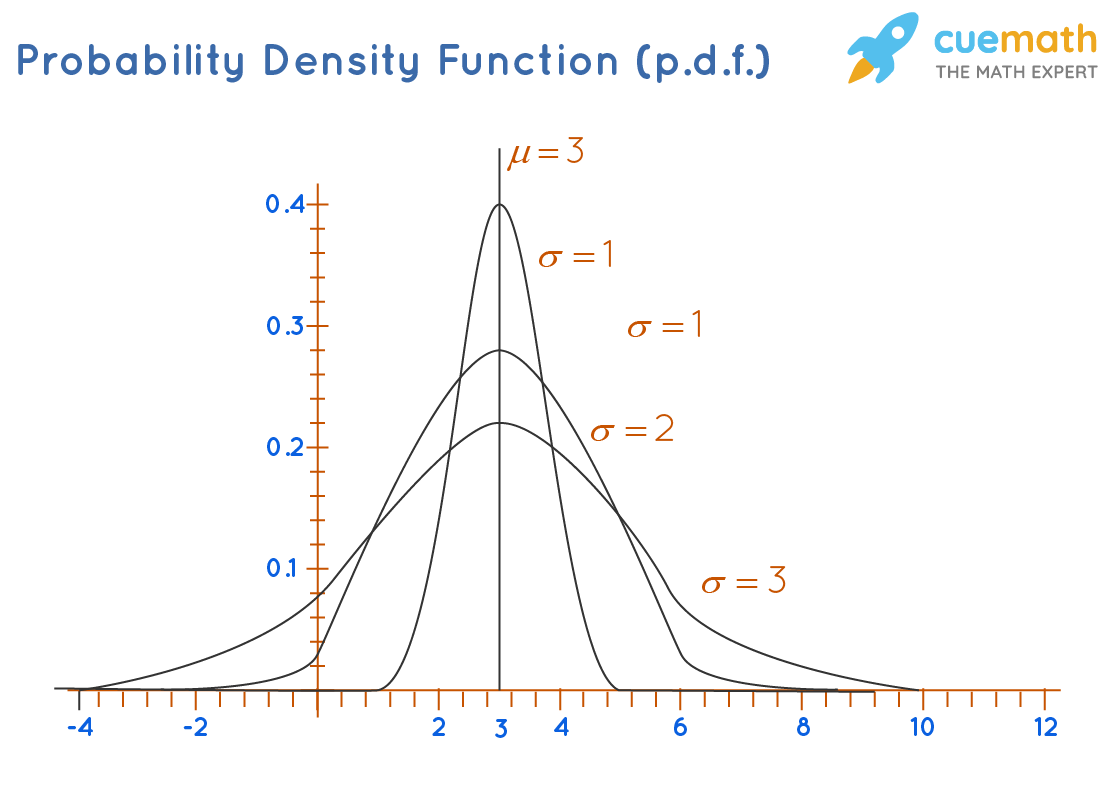
For a specific μ = 3 and a σ ranging from 1 to 3, the probability density function (p.d.f.) is as:

The probability density function of normal or gaussian distribution is given by;
\(f(x, \mu, \sigma)=\frac{1}{\sigma \sqrt{2 \pi}} e^{\frac{-(x-\mu)^{2}}{2 \sigma^{2}}}\)
Where,
\(\mathrm{x}\) is the variable
\(\mu\) is the mean
\(\sigma\) is the standard deviation

Examples using Normal Distribution Formula

Example 1: If \( X\sim N( 4 ,9) \), find \( P(X>6) \) using normal distribution formula.

Solution:
When a variable X follows a normal distribution, with mean μ and variance σ², this is denoted by: 
\( X\sim N( {\pi ,\sigma ^2 }) \)
To use normal distribution formula, let \(Z = \frac{{X - \mu }}{\sigma }=\frac{{X - 4 }}{3}\)
Hence,
\(P\left( {X > 6} \right) = 1 - P\left( {X < 6} \right) \\ = 1 - \varphi \left( {\frac{{6 - 4}}{3}} \right) \\ = 1 - \varphi \left( {0.67} \right) \\ = 1 - 0.74857 \\ = 0.25143\)
Answer: \( P(X>6)=0.25143 \)

Example 2: The working lives of a particular brand of electric light bulb are distributed with a mean of 1200 hours and a standard deviation of 200 hours. What is the probability of a bulb lasting more than 1150 hours? Use normal distribution formula.

Solution:
Let X, the working life, is distributed using normal distribution formula as, 
\(X\sim N( {1200,200^2 }) \)

Hence, 
\(  P\left( {X > 1150} \right) = 1 - P\left( {X < 1150} \right) \\ = 1 - \varphi \left( {\frac{1150 - 1200}{200}} \right) \\ = 1 - \varphi \left( {-0.25} \right) \\ = 0.59871\)

Answer: The probability of a bulb lasting more than 1150 hours is 0.59871.

Example 3: What will be the probability density function of normal distribution for the data; \(x=3, \mu=\) 4 and \(\sigma=2\)?
Solution: Given, variable, x=3
Mean =4 and
Standard deviation =2
By the formula of the probability density of normal distribution, we can write;
\(f(3,4,2)=\frac{1}{2 \sqrt{2 \pi}} e^{\frac{-(3-2)^{2}}{2 \times 2^{2}}}\)
Answer: Hence, \(f(3,4,2)=1.106\).