Mean Deviation
Mean deviation is used to compute how far the values in a data set are from the center point. Mean, median, and mode all form center points of the data set. In other words, the mean deviation is used to calculate the average of the absolute deviations of the data from the central point. Mean deviation can be calculated for both grouped and ungrouped data.
Mean deviation is a simpler measurement of variability as compared to standard deviation. When we want to find the average deviation from the data's center point, the mean deviation is used. In this article, we will take an in-depth look at mean deviation, its formula, examples as well as the merits and demerits.
What is Mean Deviation?
Mean Deviation falls under average absolute deviation. The average absolute deviation can be defined as the average of the absolute deviations from the central point of the data. The central point can be computed by using either mean, median, or mode.
Mean Deviation Definition
The difference between the observed value of a data point and the expected value is known as deviation in statistics. Thus, mean deviation or mean absolute deviation is the average deviation of a data point from the mean, median, or mode of the data set. Mean deviation can be abbreviated as MAD.
Mean Deviation Example
Suppose we have a set of observations given by {2, 7, 5, 10} and we want to calculate the mean deviation about the mean. We find the mean of the data given by 6. Then we subtract the mean from each value, take the absolute value of each result and add them up to get 10. Finally, we divide this value by the total number of observations (4) to get the mean deviation as 2.5.
Mean Deviation Formula
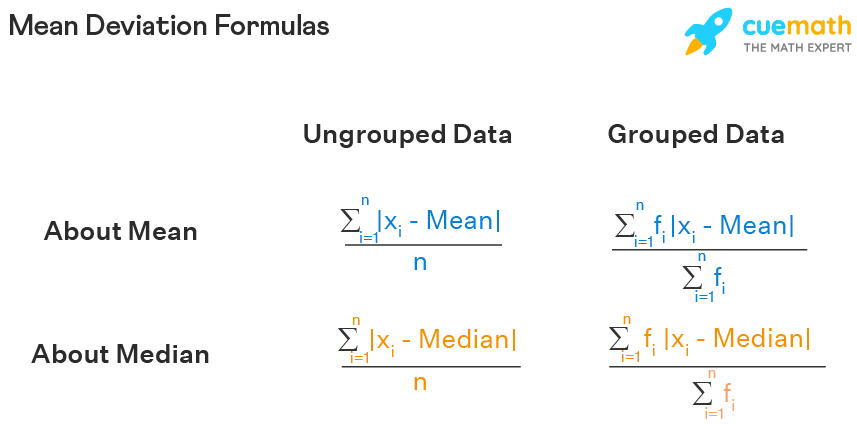
Depending upon the type of data available as well as the type of the central point, there can be several different formulas to calculate the mean deviation. Given below are the different mean deviation formulas.
Mean Deviation Formula for Ungrouped Data
Data that is not sorted or classified into groups and remains in raw form is known as ungrouped data. To calculate the mean deviation for ungrouped data the formula is as follows:
MAD = \(\frac{\sum_{1}^{n}|x_{i} - \overline{x}|}{n}\)
Here, \(x_{i}\) represents the ith observation, \(\overline{x}\) represents the central point (mean, median, or mode), and 'n' is the number of observations in the data set.
Mean Deviation Formula for Grouped Data
When data is organized and classified into groups it is known as grouped data. Grouping of data is done by continuous and discrete frequency distributions. The mean deviation formulas for grouped data are given below:
Mean Deviation for Continuous Frequency Distribution
Such a type of grouped data consists of class intervals. The frequency of repetition of an observation within each interval is given by the continuous frequency distribution. The mean deviation formula is as follows:
MAD = \(\frac{\sum_{1}^{n}f_{i}|x_{i}-\overline{x}|}{\sum_{1}^{n}f_{i}}\)
\(f_{i}\) is the frequency of repetition of \(x_{i}\). \(x_{i}\) denotes the mid value of the class interval.
Mean Deviation for Discrete Frequency Distribution
In this type of data, the individual data points are specified and the frequency with which they occur is also mentioned. To calculate the mean deviation for a discrete frequency distribution, the formula is given as follows:
MAD = \(\frac{\sum_{1}^{n}f_{i}|x_{i}-\overline{x}|}{\sum_{1}^{n}f_{i}}\)
\(x_{i}\) denotes the specified individual value and \(f_{i}\) is the frequency of occurrence of that value.
Mean Deviation about Mean
The mean is also known as the expected value of a data set. The simple definition of mean is given as the sum of all observations divided by the total number of observations. The formulas for mean deviation about the mean are given below:
- Ungrouped data MAD = \(\frac{\sum_{1}^{n}|x_{i} - \mu|}{n}\)
where, mean is \(\mu\) = \(\frac{x_{1} + x_{2} +...+x_{n}}{n}\)
- Continuous and discrete frequency distribution MAD = \(\frac{\sum_{1}^{n}f_{i}|x_{i}-\mu|}{\sum_{1}^{n}f_{i}}\)
where, mean of grouped data is \(\mu\) = \(\frac{\sum_{1}^{n}x_{i}f_{i}}{\sum_{1}^{n}f_{i}}\)
Mean Deviation about Median
Median is the value that separates the lower half of the data from the upper half. Given below are the various formulas for the mean deviation about the median:
- Ungrouped data MAD = \(\frac{\sum_{1}^{n}|x_{i} - M|}{n}\)
where, if n is odd, then median M = (\(\frac{n + 1}{2})\)th observation.
if n is even, then median M = \(\frac{\frac{n}{2}^{th}obs + (\frac{n}{2}+1)^{th}obs}{2}\)
- Discrete frequency distribution MAD = \(\frac{\sum_{1}^{n}f_{i}|x_{i}-M|}{\sum_{1}^{n}f_{i}}\)
The median is calculated in the same way as ungrouped data.
- Continuous frequency distribution MAD = \(\frac{\sum_{1}^{n}f_{i}|x_{i}-M|}{\sum_{1}^{n}f_{i}}\)
Median of grouped data M = \(l + \frac{\frac{\sum_{1}^{n}f_{i}}{2}-cf}{f}\times h\)
cf stands for cumulative frequency preceding the median class, l is the lower value of the median class, h is the length of the median class and f is the frequency of the median class.
Mean Deviation about Mode
Mode is defined as that value that occurs most frequently in a given data set. The formulas to calculate mean deviation about mode are as follows:
- Ungrouped data MAD = \(\frac{\sum_{1}^{n}|x_{i} - mode|}{n}\)
where mode = the most frequently occurring value in a data set.
- Discrete frequency distribution MAD = \(\frac{\sum_{1}^{n}f_{i}|x_{i}-mode|}{\sum_{1}^{n}f_{i}}\)
The mode can be calculated in the same way as ungrouped data
- Continuous frequency distribution MAD = \(\frac{\sum_{1}^{n}f_{i}|x_{i}-mode|}{\sum_{1}^{n}f_{i}}\)
where, mode of grouped data = \(l +(\frac{f-f_{1}}{2f - f_{1}-f_{2}})\times h\)
l is the lower value of the modal class, h is the size of the modal class, f is the frequency of the modal class, \(f_{1}\) is the frequency of the class preceding the modal class, and \(f_{2}\) is the frequency of the class succeeding the modal class.
How to Calculate Mean Deviation?
Regardless, of whether the mean deviation about the mean, median or mode needs to be determined, the general steps remain the same. The only difference will be in the formulas used to calculate the mean, median or mode depending upon the type of data available to us. Suppose the mean deviation about the mean has to be determined for the data set {10, 15, 17, 15, 18, 21}. Then the below-given steps can be followed.
- Step 1: Calculate the value of the mean, mode, or median of the given data values. Here, we find the mean given by 16.
- Step 2: Subtract the value of the central point (here, mean) from each data point. (10 - 16), (15 - 16), ..., (21 - 16) = -6, -1, 1, -1, 2, 5.
- Step 3: Now take the absolute of the values obtained in step 2. The values are 6, 1, 1, 1, 2, 5
- Step 4: Take the sum of all the values obtained in step 3. This gives 6 + 1 + 1 + 1 + 2 + 5 = 16
- Step 5: Divide this value by the total number of observations. This results in the mean deviation. As there are 6 observations hence, 16 / 6 = 2.67 which is the mean deviation about the mean.
Mean Deviation and Standard Deviation
Both mean deviation and standard deviation help to measure the variability of data. Given below is the table of differences between mean deviation and standard deviation.
| Mean Deviation | Standard Deviation |
| We use the central points (mean, median, or mode) to find the mean deviation. | We only use the mean to find the standard deviation. |
| We take the absolute value of the deviations to find the mean deviation. | To find the standard deviation, we use the square of the deviations. |
| It is less frequently used. | It is the most common measure of variability and is more frequently used. |
| If the data has a greater number of outliers, mean absolute deviation is used. | If there are a lesser number of outliers in the data, then standard deviation is used. |
Merits and Demerits of Mean Deviation
Mean deviation is a statistical measure and hence, has its merits and demerits. It is utilized in checking the spread of data with respect to the central value.
Merits of Mean Deviation
Mean deviation is a useful measure as it can remove the shortcomings of other types of statistical measures. Some of the merits are given below:
- It is easy to calculate and simple to understand.
- It does not get extremely affected by outliers.
- It is widely used in business and commerce.
- It has the least sample fluctuations as compared to other statistical measures.
- It is a good comparison measure as it is based on the deviations from the mid-value.
Demerits of Mean Deviation
Mean deviation is not capable of further algebraic treatment hence, this can lead to reduced usability. Other demerits of mean deviation are listed below:
- It is not rigidly defined as it can be calculated with respect to mean, median, and mode.
- Sociological studies rarely use this measure to analyze data.
- Negative and positive signs are ignored because we take the absolute value. This can lead to inaccuracies in the result.
Related Articles:
Important Notes on Mean Deviation
- Mean deviation is a statistical measure used to give the average value of the absolute deviation with respect to the central point of the data.
- Mean deviation can be calculated about the mean, median, and mode.
- The general formula to calculate the mean deviation for ungrouped data is \(\frac{\sum_{1}^{n}|x_{i} - \overline{x}|}{n}\) and grouped data is \(\frac{\sum_{1}^{n}f_{i}|x_{i}-\overline{x}|}{\sum_{1}^{n}f_{i}}\).
- Mean deviation is less frequently used as compared to standard deviation.
Examples on Mean Deviation
- Example 1: Find the mean deviation about the median for the following data.
Class Frequency (f) 15 - 25 12 25 - 35 6 35 - 45 9 45 - 55 4 55 - 65 2
Solution:Class f cf \(x_{i}\) |x - \(\overline{x}\)| f.|x - \(\overline{x}\)| 15 - 25 12 12 20 12.5 150 25 - 35 6 18 30 2.5 15 35 - 45 9 27 40 7.5 67.5 45 - 55 4 31 50 17.5 70 55 - 65 2 33 60 27.5 55 Total N = 33 357.5
To find the median class,
N/2 = 33/2 = 16.5
The cf value that is nearest to 16.5 but higher than it is 18.
Thus, median class is 25 - 35.
l = 25, h = 10, f = 6, cf = 12, \(\frac{\sum_{1}^{5} f_{i}}{2}\) = 16.5
Substituting these values in the formula,
M = \(l + \frac{\frac{\sum_{1}^{5}f_{i}}{2}-cf}{f}\times h\) = 32.5
Mean deviation about median = \(\frac{\sum_{1}^{5}f_{i}|x_{i}-M|}{\sum_{1}^{5}f_{i}}\) = 357.5 / 33 = 10.83
Answer: Mean deviation about median = 10.83 - Example 2: Find the mean deviation about the mean for the given data
x f 12 7 9 3 6 8 18 1 10 2
Solution:x f x.f |x - \(\overline{x}\)| f.|x - \(\overline{x}\)| 12 7 84 2.619 18.33 9 3 27 0.381 1.143 6 8 48 3.381 27.048 18 1 18 8.619 8.619 10 2 20 0.619 1.238 Total 21 197 56.378 Mean is given by \(\mu\) = \(\frac{\sum_{1}^{5}x_{i}f_{i}}{\sum_{1}^{5}f_{i}}\) = 9.381
Substituting values in the equation, MAD = \(\frac{\sum_{1}^{5}f_{i}|x_{i}-\mu |}{\sum_{1}^{5}f_{i}}\) = 56.378/21 = 2.684
Answer: The mean deviation about mean is 2.684 -
Example 3: Find the mean deviation about the mean for {12, 20, 32, 16, 5}
Solution: The data is ungrouped, thus mean = (12 + 20 + 32 + 16 + 5) / 5 = 17x |x - \(\overline{x}\)| 12 5 20 3 32 15 16 1 5 12 Total 36
Using the formula, \(\frac{\sum_{1}^{5}|x_{i} - \mu|}{5}\) = 36 / 5 = 7.2Answer: Mean deviation about mean = 7.2

FAQs on Mean Deviation
What is Mean Deviation in Statistics?
In statistics, the mean deviation is used to give the spread of data about the central point (mean, median or mode). It is a type of average absolute deviation.
What is the Formula of Mean Deviation?
The formulas for mean deviation are listed below:
- Ungrouped data MAD = \(\frac{\sum_{1}^{n}|x_{i} - \overline{x}|}{n}\).
- Grouped data MAD = \(\frac{\sum_{1}^{n}f_{i}|x_{i}-\overline{x}|}{\sum_{1}^{n}f_{i}}\).
\(\overline{x}\) denotes either the mean, median or mode depending upon what needs to be computed.
How to Calculate Mean Deviation for Grouped Data?
There can be two types of grouped data - discrete and continuous frequency distributions. The mean deviation for both can be calculated using the formula \(\frac{\sum_{1}^{n}f_{i}|x_{i}-\mu|}{\sum_{1}^{n}f_{i}}\). The mean for such type of data is given by \(\mu\) = \(\frac{\sum_{1}^{n}x_{i}f_{i}}{\sum_{1}^{n}f_{i}}\).
Is Mean Deviation a Measure of Central Tendency?
Mean deviation is not a measure of central tendency. However, it gives the spread of data about the different measures of central tendency such as mean, median, or mode.
Is Mean Deviation a Measure of Dispersion?
Mean deviation is a measure of dispersion. It helps to determine the variability of data with respect to the central value of the given data set.
Is Mean Deviation and Standard Deviation the Same?
No, mean deviation and standard deviation are not the same. Mean deviation calculates the absolute deviations from the central point of the data. However, standard deviation calculates the square of deviations from the mean of the given data.
What are the Advantages and Disadvantages of Mean Deviation?
Mean deviation is very easy to understand and does not get affected greatly by outliers or extreme points in the data. On the other hand, it is not rigidly defined and ignores the negative sign of the data by taking the absolute value.
visual curriculum