Measures of Central Tendency
Measures of central tendency describe a set of data by identifying the central position in the data set as a single representative value. There are generally three measures of central tendency, commonly used in statistics- mean, median, and mode. Mean is the most common measure of central tendency used to describe a data set.
We come across new data every day. We find them in newspapers, articles, in our bank statements, mobile and electricity bills. Now the question arises whether we can figure out some important features of the data by considering only certain representatives of the data. This is possible by using measures of central tendency. In the following sections, we will look at the different measures of central tendency and the methods to calculate them.
What are Measures of Central Tendency?
Measures of central tendency are the values that describe a data set by identifying the central position of the data. There are 3 main measures of central tendency - Mean, Median and Mode.
- Mean- Sum of all observations divided by the total number of observations.
- Median- The middle or central value in an ordered set.
- Mode- The most frequently occurring value in a data set.
Measures of Central Tendency Definition
The central tendency is defined as the statistical measure that can be used to represent the entire distribution or a dataset using a single value called a measure of central tendency. Any of the measures of central tendency provides an accurate description of the entire data in the distribution.
Measures of Central Tendency Example
Let us understand the concept of the measures of central tendency using an example. The monthly salary of an employee for the 5 months is given in the table below,
| Month | Salary |
| January | $105 |
| February | $95 |
| March | $105 |
| April | $105 |
| May | $100 |
Suppose, we want to express the salary of the employee using a single value and not 5 different values for 5 months. This value that can be used to represent the data for salaries for 5 months here can be referred to as the measure of central tendency. The three possible ways to find the central measure of the tendency for the above data are,
Mean: The mean salary of the given salary can be used as on of the measures of central tendency, i.e., x̄ = (105 + 95 + 105 + 105 + 100)/5 = $102.
Mode: If we use the most frequently occurring value to represent the above data, i.e., $105, the measure of central tendency would be mode.
Median: If we use the central value, i.e., $105 for the ordered set of salaries, given as, $95, $100, $105, $015, $105, then the measure of central tendency here would be median.
We can use the following table for reference to check the best measure of central tendency suitable for a particular type of variable:
| Type of Variable | Best Suitable Measure of Central Tendency |
| Nominal | Mode |
| Ordinal | Median |
| Interval/Ratio (not skewed) | Mean |
| Interval/Ratio (skewed) | Median |
Let us study the following measures of central tendency, their formulas, usage, and types in detail below.
- Mean
- Median
- Mode
Mean as a Measure of Central Tendency
The mean (or arithmetic mean) often called the average is most likely one of the measures of central tendency that you are most familiar with. It is also known as average. Mean is simply the sum of all the components in a group or collection, divided by the number of components.
We generally denote the mean of a given data-set by x̄, pronounced “x bar”. The formula to calculate the mean for ungrouped data to represent it as the measure is given as,
For a set of observations: Mean = Sum of the terms/Number of terms
For a set of grouped data: Mean, x̄ = Σfx/Σf
where,
- x̄ = the mean value of the set of given data.
- f = frequency of each class
- x = mid-interval value of each class
Example: The weights of 8 boys in kilograms: 45, 39, 53, 45, 43, 48, 50, 45. Find the mean weight for the given set of data.
Therefore, the mean weight of the group:
Mean = Sum of the weights/Number of boys
= (45 + 39 + 53 + 45 + 43 + 48 + 50 + 45)/8
= 368/8
= 46
Thus, the mean weight of the group is 46 kilograms.
When Not to Use the Mean as the Measure of Central Tendency?
Using mean as the measure of central tendency brings out one major disadvantage, i.e., mean is particularly sensitive to outliers. This is for the case when the values in a data are unusually larger or smaller compared to the rest of the data.
Median as a Measure of Central Tendency
Median, one of the measures of central tendency, is the value of the given data-set that is the middle-most observation, obtained after arranging the data in ascending order is called the median of the data. The major advantage of using the median as a central tendency is that it is less affected by outliers and skewed data. We can calculate the median for different types of data, grouped data, or ungrouped data using the median formula.
For ungrouped data: For odd number of observations, Median = [(n + 1)/2]th term. For even number of observations, Median = [(n/2)th term + ((n/2) + 1)th term]/2
For grouped data: Median = l + [((n/2) - c)/f] × h
where,
l = Lower limit of the median class
c = Cumulative frequency
h = Class size
n = Number of observations
Median class = Class where n/2 lies
Let us use the same example given above to find the median now.
Example: The weights of 8 boys in kilograms: 45, 39, 53, 45, 43, 48, 50, 45. Find the median.
Solution:
Arranging the given data set in ascending order: 39, 43, 45, 45, 45, 48, 50, 53
Total number of observations = 8
For even number of observation, Median = [(n/2)th term + ((n/2) + 1)th term]/2
⇒ Median = (4th term + 5th term)/2 = (45 + 45)/2 = 45
Mode as a Measure of Central Tendency
Mode is one of the measures of the central tendency, defined as the value which appears most often in the given data, i.e. the observation with the highest frequency is called the mode of data. The mode for grouped data or ungrouped data can be calculated using the mode formulas given below,
Mode for ungrouped data: Most recurring observation in the data set.
Mode for grouped data: L + h \(\frac{\left(f_{m}-f_{1}\right)}{\left(f_{m}-f_{1}\right)+\left(f_{m}-f_{2}\right)}\)
where,
- L is the lower limit of the modal class
- h is the size of the class interval
- f\(_m\) is the frequency of the modal class
- f\(_1\) is the frequency of the class preceding the modal class
- f\(_2\) is the frequency of the class succeeding the modal class
Example: The weights of 8 boys in kilograms: 45, 39, 53, 45, 43, 48, 50, 45. Find the mode.
Solution:
Since the mode is the most occurring observation in the given set.
Mode = 45
Empirical Relation Between Measures of Central Tendency
The three measures of central tendency i.e. mean, median, and mode are closely connected by the following relations (called an empirical relationship).
2Mean + Mode = 3Median
For instance, if we are asked to calculate the mean, median, and mode of continuous grouped data, then we can calculate mean and median using the formulae as discussed in the previous sections and then find mode using the empirical relation.
Example: The median and mode for a given data set are 56 and 54 respectively. Find the approximate value of the mean for this data set.
2Mean + Mode = 3Median
2Mean = 3Median - Mode
2Mean = 3 × 56 - 54
2Mean = 168 - 54 = 114
Mean = 57
Measures of Central Tendency and Type of Distribution
Any data set is a distribution of 'n' number of observations. The best measure of the central tendency of any given data depends on this type of distribution. Some types of distributions in statistics are given as,
- Normal Distribution
- Skewed Distribution
Let us understand how the type of distribution can affect the values of different measures of central tendency.
Measures of Central Tendency for Normal Distribution
Here is the frequency distribution table for a set of data:
| Observation | 6 | 9 | 12 | 15 | 18 | 21 |
| Frequency | 5 | 10 | 15 | 10 | 5 | 0 |
We can observe the histogram for the above-given symmetrical distribution as shown below,
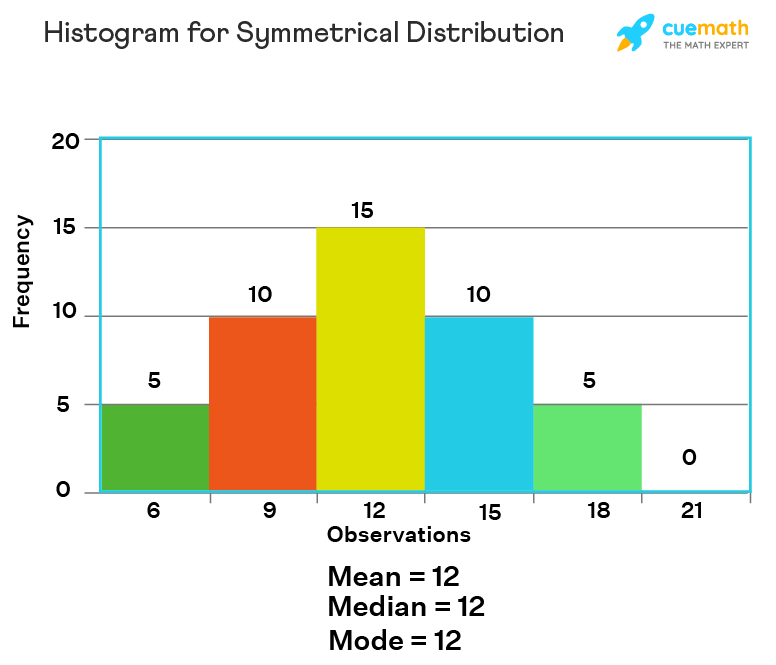
The above histogram displays a symmetrical distribution of data. Finding the mean, median, and mode for this data-set, we observe that the three measures of central tendency mean, median, and mode are all located in the center of the distribution graph. Thus, we can infer that in a perfectly symmetrical distribution, the mean and the median are the same. The above-given example had one mode, i.e, it is a unimodal set, and therefore the mode is the same as the mean and median. In a symmetrical distribution that has two modes, i.e. the given set is bimodal, the two modes would be different from the mean and median.
Measures of Central Tendency for Skewed Distribution
For skewed distributions, if the distribution of data is skewed to the left, the mean is less than the median, which is often less than the mode. If the distribution of data is skewed to the right, then the mode is often less than the median, which is less than the mean. Let us understand each case using different examples.
Measures of Central Tendency for Right-Skewed Distribution
Consider the following data-set and plot the histogram for the same to check the type of distribution.
| Observation | 6 | 9 | 12 | 15 | 18 | 21 |
| Frequency | 17 | 19 | 8 | 5 | 3 | 2 |

We observe the given data set is an example of a right or positively skewed distribution. Calculating the three measures of central tendency, we find mean = 10, median = 9, and mode = 9. We, therefore, infer that if the distribution of data is skewed to the right, then the mode is, lesser than the mean. And median generally lies between the values of mode and mean.
Measures of Central Tendency for Left-Skewed Distribution
Consider the following data-set and plot the histogram for the same to check the type of distribution.
| Observation | 6 | 9 | 12 | 15 | 18 | 21 |
| Frequency | 2 | 13 | 5 | 10 | 15 | 19 |
We observe the given data set is an example of left or negatively skewed distribution. Calculating the three measures of central tendency, we find mean = 15.75, median = 18, and mode = 21. We, therefore, infer that if the distribution of data is skewed to the left, then the mode is, greater than the median, which is greater than the mean.
Let us summarize the above observations using the graphs given below.

Related Articles:
- Summary statistics
- Frequency Distribution
- Data Collection Methods
- Graphs in Statistics
- How to Find Median
Important Notes on Measures of Central Tendency:
- The three most common measures of central tendency are mean, median, and mode.
- Mean is simply the sum of all the components in a group or collection, divided by the number of components.
- The value of the middle-most observation obtained after arranging the data in ascending order is called the median of the data.
- The value which appears most often in the given data i.e. the observation with the highest frequency is called the mode of data.
- The three measures of central tendency i.e. mean, median and mode are closely connected by the following relations (called an empirical relationship): 2Mean + Mode = 3Median
Examples on Measures of Central Tendency
-
Example 1: The mean monthly salary of 10 workers of a group is $1445. One more worker whose monthly salary is $1500 has joined the group. Find the mean monthly salary of 11 workers of the group using the measures of central tendency formula.
Solution:
Here, n=10, x̅ =1445
Using the formula,
x̅ = ∑f\(_i\)x\(_i\)/n
Therefore ∑x\(_i\) = x̅ × n
∑x\(_i\) =1445 ×10
=14450
10 workers salary = $14450
11 workers salary = $14450 + 1500 = $15950
Average salary = 15950/11
=1450
Answer: Average salary of 11 workers = $1450 -
Example 2: The following table indicates the data on the number of patients visiting a hospital in a month. Find the average number of patients visiting the hospital in a day using the measures of central tendency formula.
Number of patients Number of days visiting hospital
0-10 3 10-20 7 20-30 10 30-40 8 40-50 5 50-60 3 Solution:
In this case, we find the class-mark (also called as mid-point of a class) for each class.
Note: Class-mark = (lower limit + upper limit) / 2
Let x\(_1\), x\(_2\), x\(_3\) . . . x\(_n\) be the class marks of the respective classes.
Hence, we get the following table
Classmark (x\(_i\)) frequency (f\(_i\)) x\(_i\)f\(_i\) 5 3 15 15 7 105 25 10 250 35 8 280 45 5 225 55 3 165 Total ∑f\(_i\) = 36 ∑f\(_i\)x\(_i\) = 1040 ∴ Mean = x = ∑x\(_i\)f\(_i\) / ∑f\(_i\) = 1040/36 = 28.89
Answer: Mean of patients visiting the hospital in a day = 28.89
-
Example 3: A survey on the heights (in cm) of 50 girls of a class was conducted at a school and the data obtained is given in the form of:
Height (in cm) 120-130 130-140 140-150 150-160 160-170 Total Number of girls 4 7 12 20 8 50 Find the mode of the above data using the measures of central tendency formula.
Solution:
Modal class = 150 - 160 [as it has maximum frequency]
l = 150, h = 10, f\(_m\) = 20, f\(_1\) = 12, f\(_2\) = 7
Mode = l + [(f\(_m\) - f\(_1\))/(2f\(_m\) - f\(_1\) - f\(_2\))] × h
= 150 + [(20 - 12)/(2 × 20 - 12 - 8)] × 10= 150 + 4
= 154
Answer: Mode = 154.

FAQs on Measures of Central Tendency
What are the Measures of Central Tendency?
Measures of central tendency are those single entities or values that describe a set of data by identifying the central position in the data set. The most common measures of central tendency are the arithmetic mean, the median, and the mode.
What are Examples of Measures of Central Tendency?
Central tendency is a statistic that represents the single value of the entire population or a dataset. Some of the important examples of measures of central tendency include mode, median, arithmetic mean and geometric mean, etc.
What is the Definition of Measures of Central Tendency?
A measure of central tendency is a single value that attempts to describe a set of data by identifying the central position within that set of data. As such, measures of central tendency are sometimes called measures of central location.
What are Good Measures of Central Tendency?
The mean is the most frequently used measure of central tendency because it uses all values in the data set to give you an average. For data from skewed distributions, the median is better than the mean because it isn't influenced by extremely large values.
Where Can We Use Measures of Central Tendency in Our Daily Affairs?
Central tendency is very useful in psychology. It lets us know what is normal or 'average' for a set of data. It also condenses the data set down to one representative value, which is useful when you are working with large amounts of data.
What is the Best Measure of Central Tendency?
The best measure of central tendency depends on the type of variables.
- Nominal type of variable distribution- mode
- Ordinal type of variable distribution- median
- Skewed type of variable distribution- mean, median
What is the Difference Between Mean and Median as Measures of Central Tendency?
The mean is the average (or arithmetic mean) of the values of a data set, whereas the median is the middlemost value of the data.
How Do you Find the Measures of Central Tendency?
The measures of central tendency can be found using the formulas of mean, median, or mode in most cases. As we know, the mean is the average of a given data set, the median is the middlemost data value and the mode represents the most frequently occurring data value in the set.
visual curriculum