Exponential Decay Formula

Before knowing the exponential decay formula, first, let us recall what is meant by an exponential decay. In exponential decay, a quantity slowly decreases in the beginning and then decreases rapidly. We use the exponential decay formula to find population decay (depreciation) and we can also use the exponential decay formula to find half-life (the amount of time for the population to become half of its size). Let us learn more about the exponential decay formula along with the solved examples 

What are Exponential Decay Formulas?

The Exponential decay formula helps in finding the rapid decrease over a period of time i.e. the exponential decrease. The exponential decay formula is used to find the population decay, half-life, radioactivity decay, etc. The general form is f(x) = a (1 - r)^x.

Where

a = initial amount

1-r = decay factor

x= time period

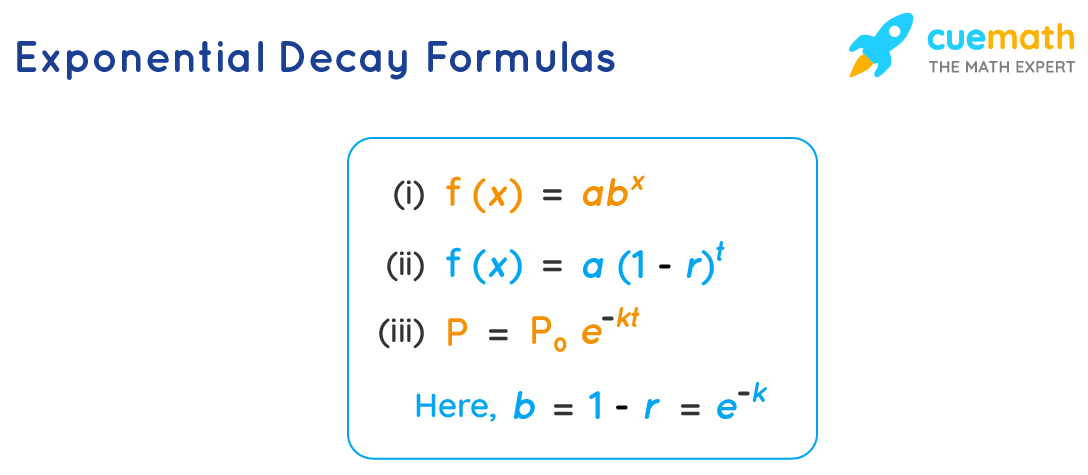
Exponential Decay Formula 

The quantity decreases slowly after which the rate of change and the rate of growth decreases over a period of time rapidly. This decrease in growth is calculated by using the exponential decay formula. The exponential decay formula can be in one of the following forms:

f(x) = ab^x

f(x) = a (1 - r)^x

P = P\(_0\) e^{-k t} 

Where,

• a (or) P\(_0\) = Initial amount
• b = decay factor
• r = Rate of decay (for exponential decay)
• x (or) t = time intervals (time can be in years, days, (or) months, whatever you are using should be consistent throughout the problem).
• k = constant of proportionality
• e- Euler's constant

Note: In exponential decay, always 0 < b < 1.Here, b = 1 - r ≈ e^{- k}.

Examples Using Exponential Decay Formulas

Example 1: Chris bought a new car for $20,000. The value of the car decreases exponentially (depreciates) at a rate of 8% per year. Then what is the value of the car after 5 years? Solve this by using exponential formulas and round your answer to the nearest two decimals.

Solution:

The initial value of the car is, P = $20,000.

The rate of decay is, r = 8% = 0.08.

The time is t = 5 years.

Using the exponential decay formula:

A = P (1 - r)^t

A = 20000 (1 - 0.08)⁵ = 13181.63

Therefore, the value of the car after 5 years = $13,181.63.

Example 2: Jane bought a new house for $350,000. The value of the house decreases exponentially (depreciates) at a rate of 5% per year. Then what is the value of the house after 2 years? Solve this by using exponential formulas and round your answer to the nearest two decimals.

Solution: 

The initial value of the house = $3,50,000

The rate of decay, r = 5% = 0.05 

The time, t = 2 years 

Using the exponential decay formula, 

A = P (1 - r)^t 

A = 350000 (1 - 0.05)²

A = 315,875

Therefore, the value of the house after 2 years = $315,875

Example 3: The half-life of carbon-14 is 5,730 years. Find the exponential decay model of carbon-14. Solve it by using the exponential decay formula and round the proportionality constant to 4 decimals.

Solution:

Using the given data, we can say that carbon-14 is decaying and hence we use the formula of exponential decay.

P = P\(_0\) e^{- k t} 

Here, P\(_0\) = initial amount of carbon

It is given that the half-life of carbon-14 is 5,730 years. It means

P = P\(_0\) / 2 = Half of the initial amount of carbon when t = 5, 730.

Substitute all these values in the formula of exponential decay:

P\(_0\) / 2 =P\(_0\) e^{- k (5730)}

Dividing both sides by P\(_0\),

0.5 = e^{- k (5730)}

Taking "ln" on both sides,

ln 0.5 = -5730k

Dividing both sides by -5730,

k = ln 0.5 / (-5730) ≈ 1.2097

Thus, the exponential decay model of carbon-14 is P = P\(_0\) e^{- 1.2097k}