Exterior Angle Formula
The exterior angle formula consists of the formulas used to calculate the exterior angles of a polygon. The exterior angle of a regular polygon is formed by extending one side of the polygon and then the angle between that extension and the adjacent side is measured. An exterior angle can be calculated if the number of sides of a regular polygon is known and can be done with the help of the exterior angle formula.

What are the Exterior Angle Formulas?
Different formulas associated with the exterior angle are given as,
- Polygon Exterior Angle Sum Theorem- Formula
The polygon exterior angle sum theorem states that the sum of all exterior angles of a convex polygon is equal to 360º.

Sum of exterior angles of polygon = 360º
The formula for the exterior angle of a regular polygon with n number of sides can be given as,
Exterior angle = 360º/n
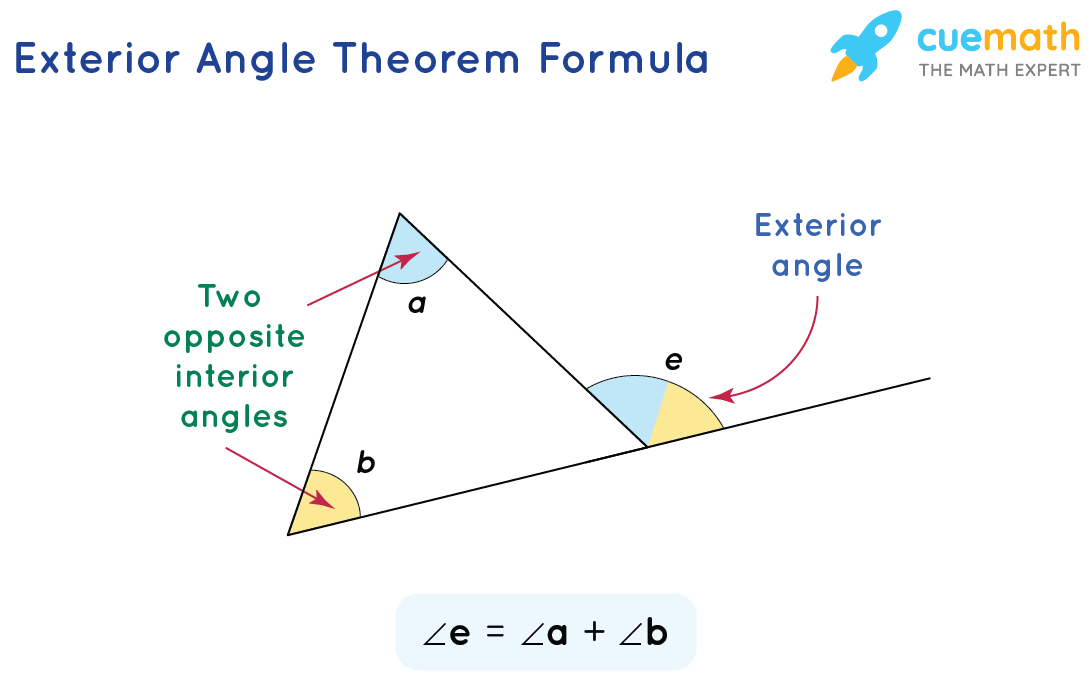
- Triangle Exterior Angle Theorem- Formula
The exterior angle theorem states that the measure of an exterior angle is equal to the sum of the measures of the two remote interior angles of the triangle. The formula for the exterior angle of any triangle can be given as,
Exterior angle = Sum of opposite interior angles
-
Example 1: Using the exterior angle theorem, find the value of x from the following figure.

Solution:
To find: Value of x
Given: Exterior angle of triangle = 160º
Using exterior angle theorem,
x + 3x = 160º
4x = 160º
x = 160º/4 = 40º
Answer: Value of x = 40º
-
Example 2: Using the exterior angle sum theorem, find the exterior angle of a regular hexagon.
Solution:
To find: Exterior angle of a regular hexagon
Given: Regular hexagon
Number of sides of a regular hexagon = 6
Using exterior angle sum theorem,
Exterior angle = 360º/6
= 60º
Answer: Exterior angle = 60º
visual curriculum