Diagonal of Rhombus
The diagonal of a rhombus is a line segment that joins any two non-adjacent vertices of a rhombus. A rhombus has two diagonals that bisect each other at right angles, thus, they form 4 right-angled triangles which are congruent. Let us learn more about the diagonal of rhombus in this article.
| 1. | What are the Diagonals of a Rhombus? |
| 2. | Diagonal of Rhombus Properties |
| 3. | Diagonal of Rhombus Formula |
| 4. | Derivation of Diagonal of Rhombus Formula |
| 5. | FAQs on Diagonal of Rhombus |
What are the Diagonals of a Rhombus?
When the opposite vertices of a rhombus are joined, they form the diagonals of a rhombus. A rhombus has two diagonals that intersect each other at 90°. Observe the following rhombus to identify its diagonals and their properties listed in the following section.
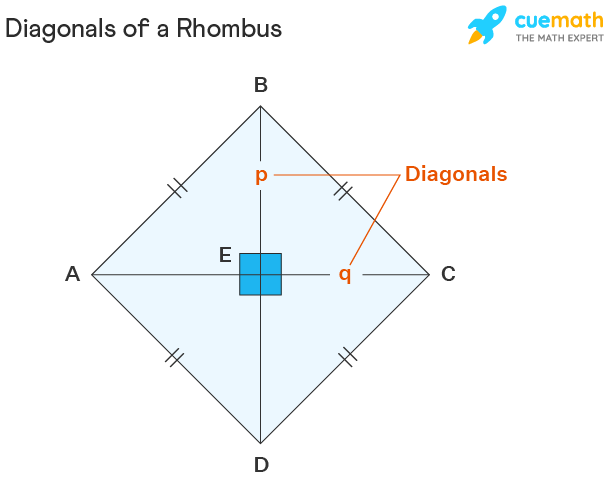
Diagonal of Rhombus Properties
The diagonals of a rhombus are line segments that are drawn between the opposite vertices of the rhombus. The properties of the diagonals of rhombus are listed below.
- The diagonals of a rhombus bisect each other at right angles.
- The diagonals of a rhombus may not be necessarily equal.
- The two diagonals divide the rhombus into four congruent right-angled triangles.
- The length of the diagonals can be calculated by various methods like using the Pythagoras theorem or by using the area of the rhombus.
Diagonal of Rhombus Formula
The formula for the diagonals of a rhombus is based on the area of the diagonals and is expressed as p = (2 × Area)/q, where 'p' and 'q' are the two diagonals of the rhombus. We know that both the diagonals bisect each other at right angles and the two diagonals divide the rhombus into four congruent right-angled triangles. Now, using these properties, let us understand how the formula to find the diagonal of a rhombus is derived.
Derivation of Diagonal of Rhombus Formula
The formula for the diagonal of a rhombus is derived using the area of the rhombus. In other words, if the area and one of the diagonals are given, then the other diagonal can be calculated using the formula, p = (2 × Area)/q, where 'p' and 'q' are the two diagonals of the rhombus. The derivation of the formula can be understood if we derive the formula for the area of a rhombus. Since we know that the diagonals of a rhombus divide it into 4 congruent right-angled triangles, the area of the rhombus will be equal to the area of all the four triangles combined together. Observe the following rhombus to see the 4 congruent right-angled triangles that can be formed in it.

Mathematically, this can be represented as,
Area of rhombus = 4 × area of one triangle
Area of rhombus = 4 × (1/2 × base × height). Now, if we take the diagonals of the rhombus to be 'p' and 'q' respectively, then the base and height in this formula can be substituted as p/2 and q/2 respectively since we know that the diagonals bisect each other.
Area of rhombus = 4 × (1/2 × p/2 × q/2)
Area of rhombus = 4 × (1/8 × p × q)
Area of rhombus = 1/2 × p × q
Now, once this formula is derived, the formula for the unknown diagonal can be derived from this. For example, if the unknown diagonal is taken to be 'p', the formula will be p = (2 × Area)/q
Important Notes on Diagonal of Rhombus
- The diagonals of rhombus bisect each other at right angles.
- The diagonals of rhombus divide the rhombus into four congruent right-angled triangles.
- A diagonal of a rhombus may not be equal to the other diagonal.
Related Articles
Examples Using Diagonal of Rhombus
-
Example 1: Find the length of the diagonal of a rhombus if the area is 54 units2, and one diagonal is 6 units.
Solution:
The area of the rhombus = 54 square units; one diagonal (q) = 6 units
We will use the formula for the diagonal of rhombus, p = (2 × Area)/q, where 'p' and 'q' are the two diagonals of the rhombus. Substituting the values, p = (2 × 54)/6 = 18 units.
Answer: Therefore, the length of the unknown diagonal is 18 units.
-
Example 2: Find the length of the second diagonal of a rhombus if the perimeter is 56 units, and one diagonal is 18 units.
Solution:
The unknown diagonal of rhombus can be calculated using the perimeter of the rhombus which is given as 56 square units; one diagonal (p) = 18 units, half of this diagonal = 18 ÷ 2 = 9 units
Since all the sides of a rhombus are equal, each side is 56 ÷ 4 = 14 units. We know that the diagonals of rhombus bisect each other at right angles. So, half of each diagonal and the side of the rhombus form a right-angled triangle. Using the Pythagoras theorem, the length of the unknown diagonal of the rhombus can be calculated.
Half of the unknown diagonal = √(142 - 92) = √(196 - 81) = √115 = 10.72 units. Since this is half the diagonal, the full length of the unknown diagonal is 10.72 + 10.72 = 21.44 units.
Answer: Therefore, the length of the unknown diagonal is 21.44 units.

FAQs on Diagonal of Rhombus
What is the Diagonal of Rhombus in Math?
The diagonal of a rhombus is the line segment that joins two opposite vertices of a rhombus. There are two diagonals in a rhombus that bisect each other at right angles.
What is the Formula of Diagonal of Rhombus?
The diagonals of a rhombus are of different lengths. They can be calculated by various methods. Let us see how to find the diagonal of a rhombus if the area of the rhombus is given. For example, if the area and one of the diagonals are known, the other diagonal can be calculated by the formula: p = (2 × Area)/q, where 'p' and 'q' are the two diagonals of the rhombus.
How to Calculate the Diagonal of Rhombus?
The diagonal of a rhombus can be calculated by various methods.
- If the area and one diagonal are given, we use the formula, p = (2 × Area)/q, where 'p' and 'q' are the two diagonals of the rhombus.
- If the perimeter and one diagonal are given, we find the side of the rhombus by dividing the perimeter by 4 since all the sides of the rhombus are equal. Since the diagonals of a rhombus bisect each other at right angles, half of each diagonal and the side of the rhombus form a right-angled triangle. Using the Pythagoras theorem, the length of the unknown diagonal can be calculated.
How to Find the Diagonal of Rhombus when Perimeter is given?
When the perimeter of a rhombus is given along with one diagonal, then the unknown diagonal can be calculated using the Pythagoras theorem. For example, if the perimeter of a rhombus is given as 100 units, and one of its diagonals is 40 units, and we need to find the other diagonal. We know that all the sides of a rhombus are equal in length, and the perimeter is 100 units, so, the length of each side is 100 ÷ 4 = 25 units. Since the diagonals of a rhombus bisect each other at right angles, therefore, we have a right-angled triangle where two sides are known and we can find the third side using the Pythagoras theorem. Half of the unknown diagonal = √(252 - 202) = √(625 - 400) = √225 = 15 units. Since this is half the diagonal, the full length of the unknown diagonal is 15 + 15 = 30 units.
How to Find the Diagonal of Rhombus when Side is given?
We know that the diagonals of a rhombus bisect each other at right angles. So, half of each diagonal and the side of the rhombus form a right-angled triangle. Using the Pythagoras theorem, the length of the unknown diagonal can be calculated.
How to Find the other Diagonal of Rhombus?
If one diagonal of a rhombus is known along with the area of the rhombus, then the other diagonal can be calculated using the formula, p = (2 × Area)/q, where 'p' and 'q' are the two diagonals of the rhombus. The given values of the area and one diagonal can be substituted to get the length of the other diagonal. For example, if the area of a rhombus is 48 square units, and one diagonal (q) is 12 units, then the other diagonal (p) can be calculated using the formula, p = (2 × Area)/q. Substituting the values, p = (2 × 48)/12 = 8 units. Therefore, the length of the other diagonal is 8 units.
visual curriculum