Find the area of the shaded region in Fig. 12.19, if PQ = 24 cm, PR = 7 cm and O is the centre of the circle
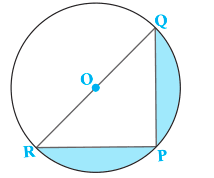
Solution:
We know that, the angle in a semicircle is a right angle.
∴ ∠RPQ = 90°
Thus, ΔRQP is a right-angled triangle.
Given, PQ = 24 cm, PR = 7 cm
∴ Using Pythagoras theorem,
RQ2 = PR2 + PQ2
RQ = √7² + 24²
= √49 + 576
= √625
Thus, PQ = 25 cm which is the diameter
∴ Radius (r) = 25/2 cm
Area of shaded region = Area of semicircle RPQ - Area of ΔRQP
= 1/2 × πr2 - 1/2 × PQ × RP
= 1/2 [(22/7 × 25/2 × 25/2) - (24 × 7)]
= 1/2 [6875/14 - 168]
= 1/2 [(6875 - 2352)/14]
= 1/2 × 4523/14
= 4523/28 cm2
= 161.54 cm2 (approximately)
☛ Check: NCERT Solutions for Class 10 Maths Chapter 12
Video Solution:
Find the area of the shaded region in Fig. 12.19, if PQ = 24 cm, PR = 7 cm and O is the centre of the circle
NCERT Solutions Class 10 Maths Chapter 12 Exercise 12.3 Question 1
Summary:
The area of the shaded region in the given figure, if PQ = 24 cm, PR = 7 cm and O is the centre of the circle is 161.54 cm2.
☛ Related Questions:
- Find the area of the shaded region in Fig. 12.20, if radii of the two concentric circles with centre O are 7 cm and 14 cm respectively and ∠ AOC = 40°.
- Find the area of the shaded region in Fig. 12.21, if ABCD is a square of side 14 cm and APD and BPC are semicircles.
- Find the area of the shaded region in Fig. 12.22, where a circular arc of radius 6 cm has been drawn with vertex O of an equilateral triangle OAB of side 12 cm as centre.
- From each corner of a square of side 4 cm a quadrant of a circle of radius 1 cm is cut and also a circle of diameter 2 cm is cut as shown in Fig. 12.23. Find the area of the remaining portion of the square.
visual curriculum