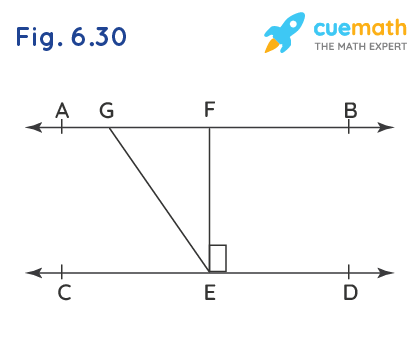
In Fig. 6.30, if AB || CD, EF ⊥ CD and ∠GED = 126°, find ∠AGE, ∠GEF and ∠FGE.
Solution:
Given: AB || CD, EF ⊥ CD and ∠GED =126°
To Find: ∠AGE, ∠GEF and ∠FGE
When two lines intersect, the sum of adjacent angles is supplementary.
When two parallel lines are cut by a transversal, alternate interior angles formed are equal.

Let ∠AGE = x, ∠GEF = y and ∠FGE = z.
From the figure, we can see that,
∠GED = ∠GEF + ∠FED
∠GEF = ∠GED - ∠FED
y = 126° - 90° [ Since, ∠GED = 126° and ∠FED = 90°]
y = 36°
Thus, ∠GEF = y = 36°
AB and CD are parallel lines cut by a transversal, thus the pair of alternate interior angles formed are equal.
∠AGE = ∠GED
Thus, ∠AGE = x = 126°
Line AB is intersected by line GE where x and z forms a linear pair.
x + z = 180°
126° + z = 180°
z = 180° - 126° = 54°
Thus, ∠FGE = z = 54°
☛ Check: NCERT Solutions Class 9 Maths Chapter 6
Video Solution:
In Fig. 6.30, if AB || CD, EF ⊥ CD and ∠GED =126°, find ∠AGE, ∠GEF and ∠FGE.
NCERT Solutions Class 9 Maths Chapter 6 Exercise 6.2 Question 3
Summary:
In Fig. 6.30, if AB || CD, EF⊥CD, and ∠GED = 126°, then the values of ∠AGE, ∠GEF, and ∠FGE are 126°, 36°, and 54° respectively.
☛ Related Questions:
- In Fig. 6.28, find the values of x and y and then show that AB||CD.
- In Fig. 6.29, if AB || CD, CD || EF and y : z = 3 : 7, find x.
- In Fig. 6.31, if PQ || ST, ∠PQR = 110° and ∠RST = 130°, find ∠QRS.[Hint: Draw a line parallel to ST through point R.]
- In Fig. 6.32, if AB || CD, ∠APQ = 50° and ∠PRD = 127°, find x and y.
visual curriculum