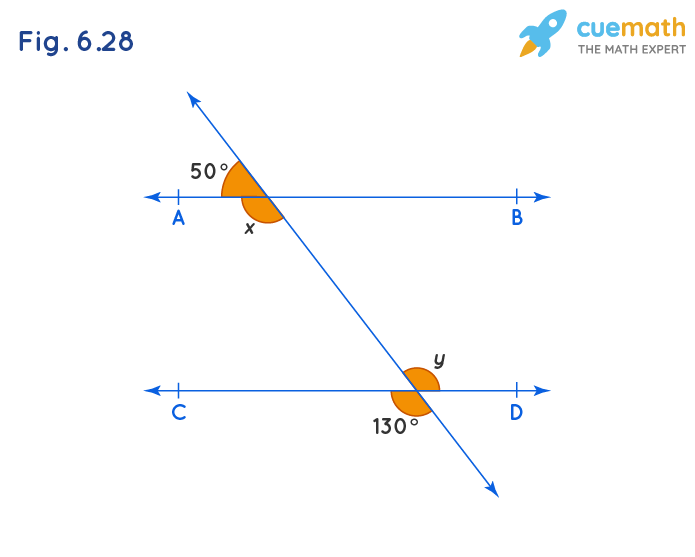
In Fig. 6.28, find the values of x and y and then show that AB || CD.

Solution:

When two lines intersect, vertically opposite angles are formed at the point of intersection which is equal.

Also, when a ray intersects a line, the sum of adjacent angles formed is 180° as it forms a linear pair.

If a transversal intersects two lines such that a pair of alternate interior angles are equal, then the two lines are parallel to each other.

Line CD is intersecting with line P. Hence the vertically opposite angles so formed are equal.

Thus, y = 130°.

Similarly, line AB is intersecting with line P forming a linear pair. Hence the sum of adjacent angles formed is 180°.

x + 50° = 180°

x = 180° - 50°

x = 130°

We know that, if a transversal intersects two lines such that a pair of alternate interior angles are equal, then the two lines are parallel.

Here we can see that the pair of alternate angles formed when lines AB and CD are intersected by transversal P are equal.

i.e, x = y = 130°. So we can say the two lines AB and CD are parallel.

Hence AB || CD is proved.

☛ Check: NCERT Solutions Class 9 Maths Chapter 6

Video Solution:

In Fig. 6.28, find the values of x and y and then show that AB || CD.

NCERT Solutions Class 9 Maths Chapter 6 Exercise 6.2 Question 1

Summary:

The value of x and y from the given figure is x = y = 130° which are alternate interior angles. Thus, the two lines AB and CD are parallel. 

☛ Related Questions:

• In Fig. 6.29, if AB || CD, CD || EF and y : z = 3 : 7, find x.
• In Fig. 6.30, if AB||CD, EF ⊥ CD and ∠GED =126°, find ∠AGE, ∠GEF and ∠FGE.
• In Fig. 6.31, if PQ || ST, ∠PQR = 110° and ∠RST = 130°, find ∠QRS.[Hint: Draw a line parallel to ST through point R.]
• In Fig. 6.32, if AB || CD, ∠APQ = 50° and ∠PRD = 127°, find x and y.