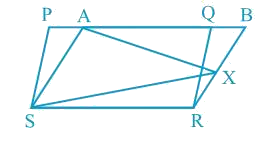
In Fig. 9.17, PQRS and ABRS are parallelograms and X is any point on side BR. Show that (i) ar (PQRS) = ar (ABRS) (ii) ar (AXS) = 1/2 ar (PQRS)
Solution:
If a triangle and a parallelogram are on the same base and between the same parallel lines, the area of the triangle will be half of that of a parallelogram or if two parallelograms are on the same and between two parallel lines then their area will be equal.
i) It can be observed from the figure that parallelogram PQRS and ABRS lie on the same base SR and also, they lie between the same parallel lines SR and PB.
According to Theorem 9.1, Parallelograms on the same base and between the same parallel lines are equal in area.
∴ Area (PQRS) = Area (ABRS) .....(1)
ii) Consider ΔAXS and parallelogram ABRS
As both lie on the same base AS as well as between the same parallel lines AS and BR, Area (ΔAXS) = 1/2 Area (ABRS) .....(2)
From Equations (1) and (2), we obtain Area (ΔAXS) = 1/2 Area (PQRS)
☛ Check: Class 9 Maths NCERT Solutions Chapter 9
Video Solution:
In Fig. 9.17, PQRS and ABRS are parallelograms and X is any point on side BR. Show that (i) ar (PQRS) = ar (ABRS) (ii) ar (AXS) = 1/2 ar (PQRS)
NCERT Maths Solutions Class 9 Chapter 9 Exercise 9.2 Question 5
Summary:
If PQRS and ABRS are parallelograms and X is any point on side BR, then Area of (PQRS) = Area of (ABRS), and Area of (AXS) = 1/2 Area of (PQRS).
☛ Related Questions:
- In Fig. 9.15, ABCD is a parallelogram, AE ⊥ DC and CF ⊥ AD. If AB = 16 cm, AE = 8 cm and CF = 10 cm, find AD.
- If E, F, G, and H are respectively the mid-points of the sides of a parallelogram ABCD, show that ar (EFGH) = 1/2 ar (ABCD).
- P and Q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that ar (APB) = ar (BQC).
- In Fig. 9.16, P is a point in the interior of a parallelogram ABCD. Show that (i) ar (APB) + ar (PCD) = 1/2 ar (ABCD) (ii) ar (APD) + ar (PBC) = ar (APB) + ar (PCD) [Hint: Through P, draw a line parallel to AB.]
visual curriculum