Parallelogram

A parallelogram is a quadrilateral in which the opposite sides are parallel and equal. Parallelograms are classified into three main types: square, rectangle, and rhombus, and each of them has its own unique properties. In this article, let us learn about the parallelogram shape, the parallelogram definition, the different types of parallelograms, how to find the area of a parallelogram and parallelogram examples.

1.	What is a Parallelogram?
2.	Properties of a Parallelogram
3.	Types of Parallelograms
4.	Parallelogram Formualas
5.	FAQs on Parallelogram

What is a Parallelogram?

A parallelogram is a special kind of quadrilateral that is formed by parallel lines. The angle between the adjacent sides of a parallelogram may vary but the opposite sides need to be parallel for it to be a parallelogram. A quadrilateral will be a parallelogram if its opposite sides are parallel and congruent.

Parallelogram Definition

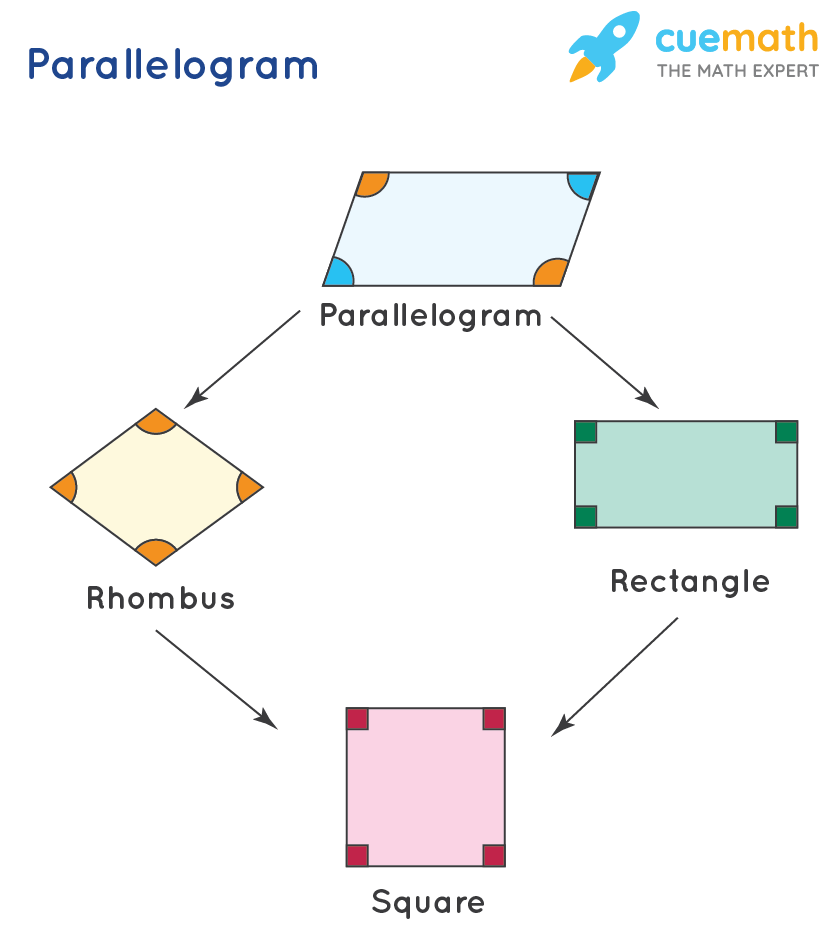
A parallelogram is defined as a quadrilateral in which both pairs of opposite sides are parallel and equal. Observe the following figure which shows the three types of parallelograms:

parallelogram examples.

Properties of a Parallelogram

There are some basic properties that help us to identify a parallelogram. Observe the following parallelogram PQTR to relate to its properties given below.

Properties of parallelogram

We can identify and distinguish a parallelogram with the help of the following properties:

The opposite sides of a parallelogram are parallel. Here, PQ ‖ RT and PR ‖ QT.
The opposite sides of a parallelogram are equal. Here, PQ = RT and PR = QT
The opposite angles of a parallelogram are equal. Here, ∠P = ∠T and ∠Q = ∠R
The diagonals of a parallelogram bisect each other. Here, RE = EQ and PE = ET
Same-side interior angles supplement each other. Here, ∠PRT + ∠RTQ = 180^∘, ∠RTQ + ∠TQP = 180^∘, ∠TQP + ∠QPR = 180^∘, ∠QPR + ∠PRT = 180^∘
The diagonals divide the parallelogram into two congruent triangles. Here, ΔRPQ is congruent to ΔQTR, and ΔRPT is congruent to ΔQTP

Types of Parallelogram

A parallelogram can be divided into various types depending upon the different properties. It is mainly divided into three special types:

Rectangle
Square
Rhombus

Let us study these parallelograms in detail.

Rectangle

A rectangle is a parallelogram with two pairs of equal and parallel opposite sides and four right angles.

A rectangle is a type of a parallelogram.

Observe the rectangle ABCD to relate it with the following properties. A rectangle has:

Two pairs of parallel sides. Here, AB || DC and AD || BC
Four right angles. Here, ∠A = ∠B = ∠C = ∠D = 90^∘
Opposite sides of equal lengths. Here, AB = DC and AD = BC
Two equal diagonals. Here, AC = BD
Diagonals that bisect each other.

Square

A square is a parallelogram with four equal sides and four right angles.

Paralellogram examples: A square is a type of a parallelogram.

Observe the square ABCD to relate it with the following properties. A square has:

Four equal sides. Here, AB = BC = CD = DA
Four right angles. Here, ∠A = ∠B = ∠C = ∠D = 90^∘
Two pairs of parallel sides. Here, AB || DC and AD || BC
Two equal diagonals. Here, AC = BD
Diagonals that are perpendicular to each other. Here, AC⊥BD
Diagonals that bisect each other.

Rhombus

A rhombus is a parallelogram with four equal sides in which the opposite angles are equal.

Parallelogram examples: A rhombus is a type of a parallelogram.

Observe the rhombus EFGH to relate it with the following properties. A rhombus has:

Two pairs of parallel sides. Here, EH || FG and EF || HG
Four equal sides. Here, EH = HG = GF= FE
Equal opposite angles. Here, ∠E = ∠G and ∠H = ∠F
Diagonals that are perpendicular to each other. Here, EG⊥HF
Diagonals that bisect each other.

Parallelogram Formulas

Every two-dimensional figure has two basic formulas area as well as the perimeter. Let us discuss these two formulas of a parallelogram in this section.

Area of Parallelogram

The area of a parallelogram is the space enclosed between the four sides of a parallelogram. It can be calculated if we know the length of the base and the height of the parallelogram and it is measured in square units like cm², m², and inch². Observe the following parallelogram which shows the base and the height.

Area of a parallelogram

Consider the parallelogram PQRS with base (b) and height (h). The area of the parallelogram is calculated with the help of the formula: Area of Parallelogram = Base (b) × Height (h)

Perimeter of Parallelogram

The perimeter of a parallelogram is the total length of its boundary and hence it is equal to the sum of all its sides.

Thus, the perimeter (P) of a parallelogram with sides is, P = 2 (a + b)

☛Related Topics

Check out the following articles related to parallelograms.

Parallelogram Examples

Example 1: In the given parallelogram ABCD, ∠A = 90^∘. Show that all its angles are equal to 90^∘.

Solution:

Applying the parallelogram properties, we know that the opposite angles are equal. Therefore, ∠A = ∠C = 90^∘

We also know that the adjacent angles of a parallelogram are supplementary. Therefore, ∠A+∠D = 180^∘

⇒ ∠D = 180^∘− 90^∘ (∵∠A = 90^∘)

∴ ∠D = 90^∘

Since all the three angles of the parallelogram are measured 90^∘, the fourth angle will also be equal to 90^∘. ∠B = 90^∘

Answer: ∠A = ∠B = ∠C = ∠D = 90^∘
Example 2: Prove that when the diagonals of a parallelogram bisect each other at 90^∘, it is a rhombus.

Solution:

Consider the parallelogram ABCD.

First, let us prove that ΔAEB and ΔAED are congruent.

AE = AE (common)

BE = ED (given)

∠AEB = ∠AED = 90^∘ (given)

Therefore, by SAS Congruency, ΔAEB and ΔAED are congruent.

⇒AB = AD

Similarly, considering congruent triangles ΔAED and ΔCED

⇒AD = DC

This shows that: AB = BC = CD = AD, which proves that this parallelogram is a rhombus.

Answer: Therefore, the given parallelogram is a rhombus.
Example 3: State true or false:

a.) The opposite sides of a parallelogram are parallel.

b.) The diagonals of a parallelogram do not bisect each other.

Solution:

a.) True, the opposite sides of a parallelogram are parallel.

b.) False, the diagonals of a parallelogram always bisect each other.

go to slide go to slide go to slide

Break down tough concepts through simple visuals.

Math will no longer be a tough subject, especially when you understand the concepts through visualizations.

Book a Free Trial Class

Practice Questions on Parallelogram

go to slide go to slide

FAQs on Parallelogram

What is a Parallelogram Shape in Geometry?

A parallelogram is a quadrilateral which is made up of 2 pairs of parallel sides. In a parallelogram, the opposite sides are parallel and equal in length. A few examples of a parallelogram are rhombus, rectangle, and square.

What is the Difference Between a Parallelogram and a Quadrilateral?

All parallelograms are quadrilaterals but all quadrilaterals are not necessarily parallelograms. For example, a trapezoid is a quadrilateral, but not a parallelogram. For a quadrilateral to be a parallelogram, all the opposite sides must be parallel and equal to each other.

What is the Perimeter of Parallelogram?

A parallelogram is a special kind of quadrilateral in which the opposite sides are parallel and equal. The perimeter of a parallelogram is the sum of the length of all its sides and it is calculated with the help of the formula: Perimeter = 2(a + b); where 'a' and 'b' are the two sides of the parallelogram.

What is the Area of a Parallelogram?

The area of a parallelogram is the region covered by its boundary. The formula for the area of a parallelogram is: Area = b × h; where 'b' is the length of the base of the parallelogram, and 'h' is the height of the parallelogram.

Is a Rhombus a Parallelogram?

Yes, a rhombus is a parallelogram in which the opposite sides are parallel and the opposite angles are congruent. Apart from this, all the sides of a rhombus are equal and the diagonals bisect each other at right angles.

Is a Trapezoid a Parallelogram?

No, a trapezoid is not a parallelogram, since all opposite sides of the trapezoid are not parallel to each other. A trapezoid has only one pair of opposite sides parallel to each other. Also, a trapezoid doesn't have opposite sides equal to each other. Hence, it is a quadrilateral but not a parallelogram.

Is a Rectangle a Parallelogram?

Yes, a rectangle is a parallelogram in which the opposite sides are parallel and equal. Apart from this, all the angles of a rectangle are congruent and it has equal diagonals that bisect each other.

What are the Three Special Parallelograms?

The three special parallelograms are rectangle, square, and rhombus. All three figures fulfill the properties of a parallelogram because they are four-sided and they have 2 pairs of sides that are parallel and equal.

Do Angles in a Parallelogram Sum Up to 360°?

Yes, all the four interior angles of a parallelogram sum up to 360°. For example, in a parallelogram ABCD, sum of ∠A + ∠B + ∠C + ∠D = 360°.

Are all the Angles of a Parallelogram Equal?

No, all the angles of a parallelogram are not equal. Only the opposite angles of a parallelogram are equal and the consecutive (adjacent) angles of a parallelogram are always supplementary.

What is the Difference Between Trapezoid and Parallelogram?

A trapezoid is different from a parallelogram since all the opposite sides of a trapezoid are not parallel to each other. A trapezoid has only one pair of opposite sides parallel to each other.

What is the Shape of a Parallelogram?

A parallelogram is a four-sided polygon in which the opposite sides are always parallel and equal.

How many Vertices does a Parallelogram have?

A parallelogram is a quadrilateral and that is why it has 4 vertices (4 corners).

Are all Parallelogram Sides Congruent?

In a parallelogram, all sides may not be necessarily congruent. The opposite sides are parallel and equal (congruent). However, square is the only parallelogram in which all sides are congruent.

How many Types of Parallelograms are there?

A parallelogram can be divided into three special types depending on the different properties that they have.