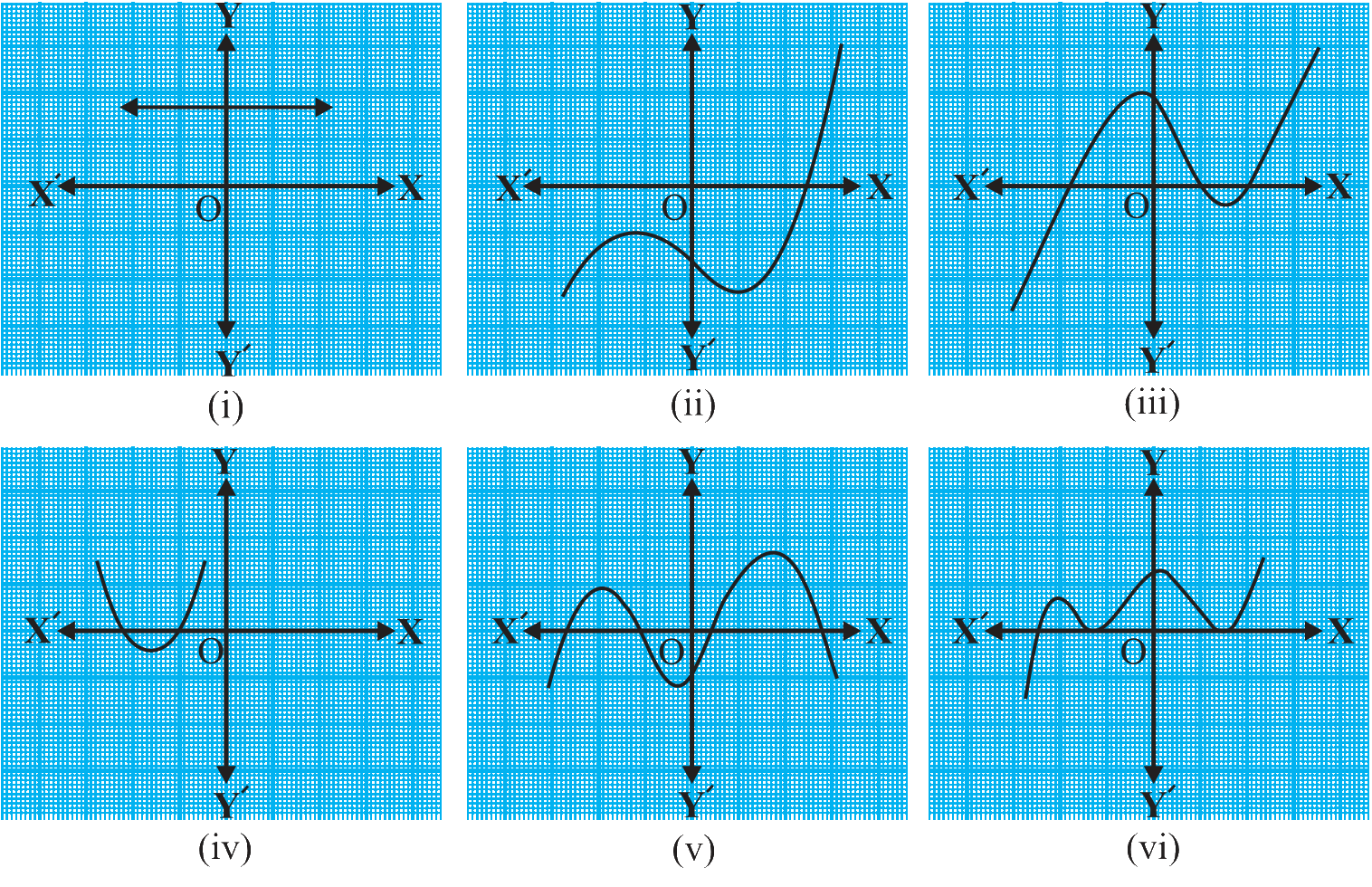
The graphs of y = p(x) are given in Fig. 2.10 below, for some polynomials p(x). Find the number of zeroes of p(x), in each case.

Solution:

We can reach the solution easily by understanding the statement of the question.

As the graphs of y = p(x) are given, and we have to find the number of zeroes of p(x), in each case, look at the graphs and visually find how many points the graph cuts or touches the x-axis.

The number of points it cuts or touches the x-axis are the zeroes of the polynomial p(x).

(i) The number of zeroes is 0 as the graph doesn’t cut the x-axis at any point.

(ii) The number of zeroes is 1 as the graph cuts the x-axis at only one point.

(iii) The number of zeroes is 3 as the graph cuts the x-axis at 3 points.

(iv) The number of zeroes is 2 as the graph cuts the x-axis at 2 points.

(v) The number of zeroes is 4 as the graph cuts the x-axis at 4 points.

(vi) The number of zeroes is 3 as the graph cuts the x-axis at 3 points.

☛ Check: Class 10 Maths NCERT Solutions Chapter 2

Video Solution:

The graphs of y = p(x) are given in Fig. 2.10 below, for some polynomials p(x). Find the number of zeroes of p(x), in each case

NCERT Solutions Class 10 Maths Chapter 2 Exercise 2.1 Question 1:

Summary:

The number of zeroes of the graphs of y = p(x) given in Fig. 2.10, for some polynomials p(x) in each case are 0, 1, 3, 2, 4, and 3 as the graphs cut the x-axis at 0, 1, 3, 2, 4, and 3 point(s) respectively.

☛ Related Questions:

• Find the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients(i) x2 - 2x - 8(ii) 4s2 - 4s + 1(iii) 6x2 - 3 - 7x(iv) 4u2 + 8u(v) t2 - 15(vi) 3x2 - x - 4
• Find a quadratic polynomial each with the given numbers as the sum and product of its zeroes respectively. (i) 1/4, - 1 (ii) √2, 1/3 (iii) 0, 5 (iv) 1, 1 (v) - 1/4, 1/4 (vi) 4, 1
• Divide the polynomial p(x) by the polynomial g(x) and find the quotient and remainder in each of the following:(i) p(x) = x3 - 3x2 + 5x - 3, g(x) = x2 - 2(ii) p(x) = x4 - 3x2 + 4x + 5, g(x) = x2 + 1 - x(iii) p(x) = x4 - 5x + 6, g(x) = 2 - x2
• Check whether the first polynomial is a factor of the second polynomial by dividing the second polynomial by the first polynomial:(i) t2 - 3, 2t4 + 3t3 - 2t2 - 9t - 12(ii) x2 + 3x + 1, 3x4 + 5x3 - 7x2 + 2x + 2(iii) x3 - 3x + 1, x5 - 4x3 + x2 + 3x + 1