Phase Shift Formula
The phase shift formula is used to find the phase shift of a function. Phase Shift is a shift when the graph of the sine function and cosine function is shifted left or right from their usual position or we can say that in phase shift the function is shifted horizontally how far from the usual position. Generally, functions are shifted (π/2) from the usual position. Let us learn more about the phase shift formula along with solved examples in the following section.

What Is Phase Shift Formula?
The phase shift formula for a sine curve is shown below where horizontal as well as vertical shifts are expressed. The phase shift can be either positive or negative depending upon the direction of the shift from the origin. Phase Shift Formula can be expressed as,
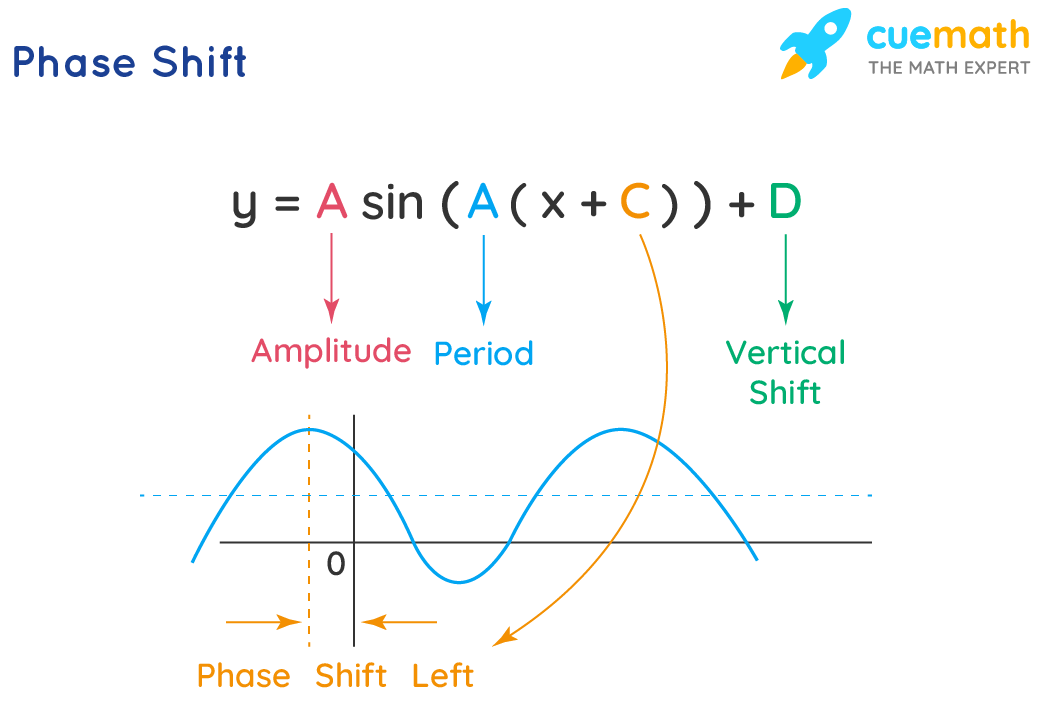
y = A sin(B(x + C)) + D
also, F(x) = Asin(Bx − C)+D.
where
- (C/B) represents the phase shift.
- A is the amplitude.
Solved Examples Using Phase Shift Formula
-
Example 1: Find out what is the phase shift of a sine having F(t)= 3 sin(4(x − 0.5)) + 2 by using the phase shift formula.
Solution:
To find: Phase shift of a sine wave
Using Phase Shift Formula,
y = A sin(B(x + C)) + D
On comparing the given equation with Phase Shift Formula
We get
Amplitude, A = 3
Period, 2π/B = 2π/4 = π/2
Vertical shift, D = 2
So, the phase shift will be −0.5
which is a 0.5 shift to the right.
Answer: The phase shift of the given sine function is 0.5 to the right.
-
Example 2: Find the phase shift of F(t)=3sin(4t+3) with the help of the phase shift formula.
Solution:
To find: Phase difference of a sine wave
Given:
Amplitude, A = 3
Period, 2π/B = 2π/4 = π/2
Vertical shift, D = 0
Using Phase Shift Formula,
F(x) = Asin(Bx−C) + D.
C/B represents the phase shift
Phase Shift= -3/4
Answer: The phase shift of the given sine function is -3/4.
visual curriculum