Quartile Formula

The quartile formula helps in calculating the value that divides a list of numbers into quarters. The data is firstly arranged into ascending order and is then divided into quartiles. Median divides a given data into two equal parts while quartiles divide it into four parts. Using the quartile formula we can find the first quartile, second quartile, and third quartile.

What Is Quartile Formula? 

The quartile formula helps to divide a set of observations into 4 equal parts. The first quartile lies in the middle of the first term and the median. The median is the second quartile. The middle value lying between the median and the last term is the third quartile. Mathematically, they are represented as follows,

When the set of observations are arranged in ascending order the quartiles are represented as,

1. First Quartile(Q1) = ((n + 1)/4)^th Term 
2. Second Quartile(Q2) = ((n + 1)/2)^th Term
3. Third Quartile(Q3) = (3(n + 1)/4)^th Term

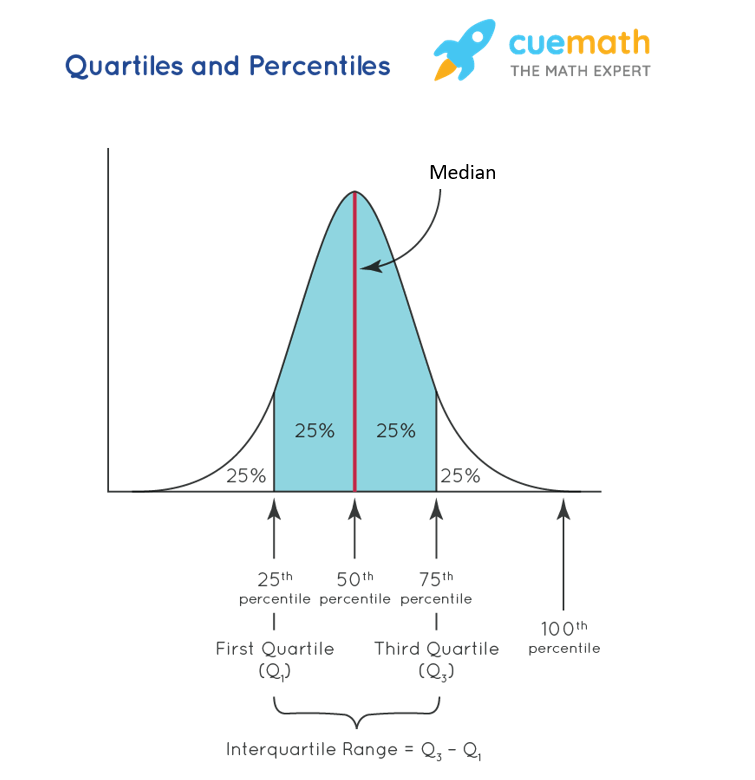
1^st quartile is also known as the lower quartile. 2^nd quartile is the same as the median dividing data into 2 equal parts. 3^rd quartile is also called the upper quartile.

The interquartile range is calculated as Upper Quartile – Lower Quartile.

Examples Using Quartile Formula

Example 1: Calculate the median, lower quartile, upper quartile, and interquartile range of the following data set of values: 20, 19, 21, 22, 23, 24, 25, 27, 26

Solution:

Arranging the values in ascending order: 19, 20, 21, 22, 23, 24, 25, 26, 27

Putting the values in the formulas above we get,

Median(Q2) = 5^th Term = 23

Lower Quartile (Q1) = Mean of 2^nd and 3^rd term = (20 + 21)/2 = 20.5

Upper Quartile(Q3) = Mean of 7^th and 8^th term = (25 + 26)/2 = 25.5

IQR = Upper Quartile−Lower Quartile

IQR = 25.5 – 20.5

IQR = 5

Answer: IQR = 5

Example 2: What will be the upper quartile for the following set of numbers?
26, 19, 5, 7, 6, 9, 16, 12, 18, 2, 1.

Solution:

The formula for the upper quartile formula is Q3 = ¾(n + 1)^th Term.

The formula instead of giving the value for the upper quartile gives us the place. For example, 8^th place, 10^th place, etc.

So firstly we put your numbers in ascending order: 1, 2, 5, 6, 7, 9, 12, 16, 18, 19, 26. There are a total of 11 numbers, so:

Q3 = ¾(n + 1)^th Term.

Q3 = ¾(12)^th Term. = 9^th Term.

Solution: The upper quartile (18) is the 9^th term or on the 9^th place from the left.

Example 3: Find the 3rd quartile in the following data set: 4, 5, 8, 7, 11, 9, 9

Solution: 

Let us first arrange our array in ascending order and it becomes 4, 5, 7, 8, 9, 9, 11

The median of our data is 8.

In order to find the 3rd quartile, we have to deal with the data points that are greater than the median that is 9, 9, 10.

In order to find the 3rd quartile, we have to find the median of the data points that are greater than the median that is 9, 9, 10.

You can use Cuemath's online quartile calculator to verify your answer.

Answer: Hence, the 3rd quartile of our data set is 9.