Identify the horizontal asymptote of f(x) = 3 over 5 x.

Solution:

If the distance between the graph of a function and some fixed-line approaches zero as a point on the graph moves increasingly far from the origin, we say that the graph approaches the line asymptotically and that line is an asymptote of the graph.

The graph of the function 3/5x is shown below:

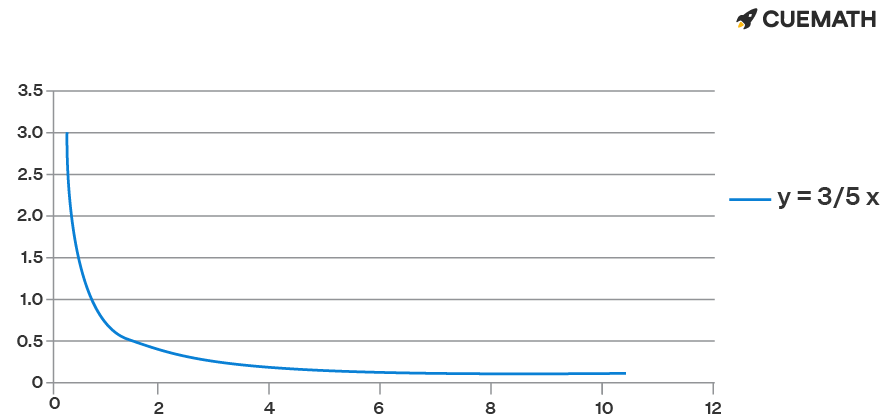
Looking at f(x) = 3/5x we observe that the x -axis is an asymptote of the curve on the right because:

\(\lim_{x\rightarrow \infty }\frac{3}{5x} = 0\)

We say that the x-axis is the horizontal asymptote of the graph of y = 3/5x.

⇒ y = 0 is the horizontal asymptote of  the graph of y = 3/5x.

Identify the horizontal asymptote of f(x) = 3 over 5 x.

Summary:

The horizontal asymptote of f(x) = 3 over 5 x is the x - axis.  y = 0 is the horizontal asymptote of  the graph of y = 3/5x.