The function f(x) = -(x + 5)(x + 1) is shown. What is the range of the function?

Solution:

Given, f(x) = -(x + 5)(x + 1)

We have to find the range of the function.

To find range, let’s substitute different values of x

If x = -5, f(-5) = -(-5 + 5)(-5 + 1) = -(0)(-4)

f(-5) = 0

If x = -4, f(-4) = -(-4 + 5)(-4 + 1) = -(1)(-3)

f(-4) = 3

If x = -3, f(-3) = -(-3 + 5)(-3 + 1) = -(2)(-2)

f(-3) = 4

If x = -2, f(-2) = -(-2 + 5)(-2 + 1) = -(3)(-1)

f(-2) = 3

If x = -1, f(-1) = -(-1 + 5)(-1 + 1) = -(4)(0)

f(-1) = 0

If x = 0, f(0) = -(0 + 5)(0 + 1) = -(5)(1)

f(0) = -5

If x = 1, f(1) = -(1 + 5)(1 + 1) = = -(6)(2)

f(1) = -12

If x = 2, f(2) = -(2 + 5)(2 + 1) = -(7)(3)

f(2) = -21

Thus, the coordinates of the function are (-5, 0), (-4, 3), (-2, 3), (-1, 0), (0, -5), (1, -12), (2, -21).

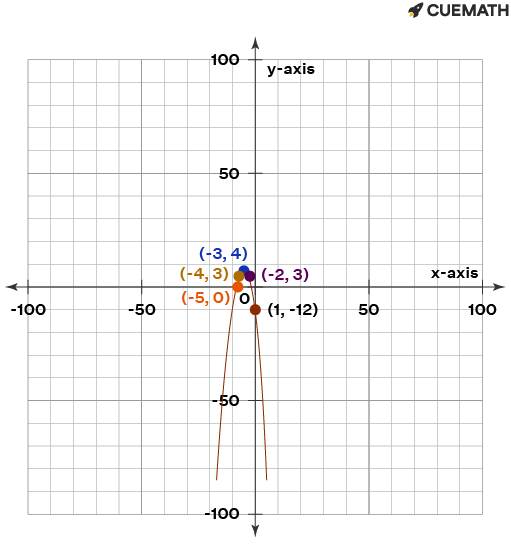
We can plot a graph using the above coordinates.

Therefore, the range of the function is all real numbers less than or equal to 4.

---

The function f(x) = -(x + 5)(x + 1) is shown. What is the range of the function?

Summary:

The function f(x) = -(x+5)(x+1) is shown. The range of the function is all real numbers less than or equal to 4.