What is the area of the shaded sector of the circle?

Solution:

A sector is a region that is bounded by two radii and the arc of the circle that lies between the radii. The area of a sector is a fraction of the area of the circle. This area is proportional to the central angle θ. This implies that the bigger the central angle, the larger is the area of the sector.

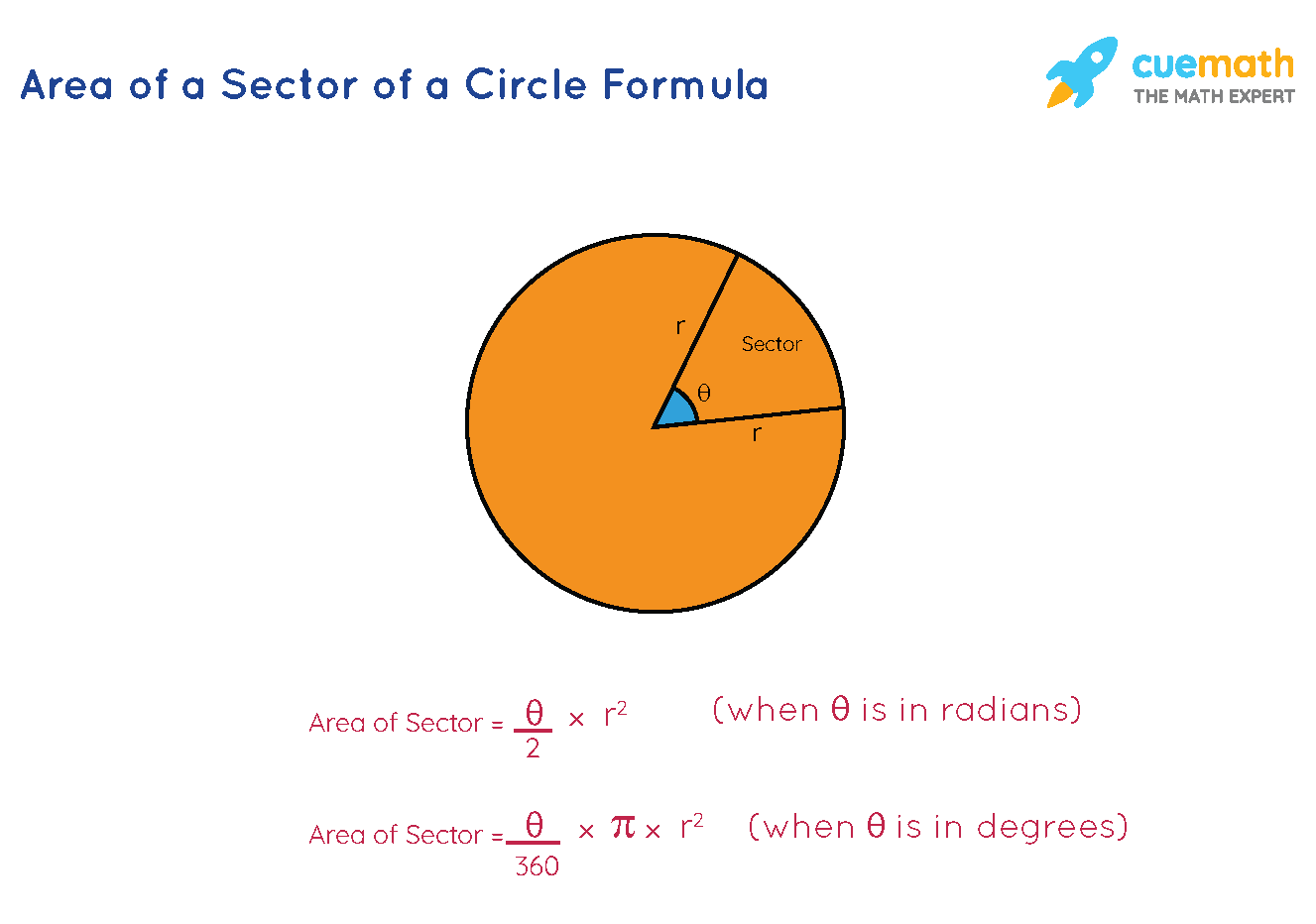
Area of a sector = (θ / 2) × r² where r = radius and θ is in radians.

or Area of a sector =  (θ / 360) × πr² where θ is in degrees.

You can use Cuemath's Area of a Sector Calculator to find the area of a sector of a circle.

So, we use the formula A = (θ / 2) × r² or (θ / 360) × πr²  is used to find the area of the sector of the circle.

What is the area of the shaded sector of the circle?

Summary:

The area of the shaded sector of the circle is A = (θ / 2) × r² where θ is in radians or (θ / 360) × πr² where θ is in degrees.