Ratio and Proportion
Ratio is used for comparing two quantities of the same kind. The ratio formula for two numbers, a and b is expressed as a : b or a/b. When two or more ratios are equal, they are said to be in proportion. The concept of ratio and proportion is based on fractions. Ratio and proportion are the key foundations for various other concepts in Mathematics. Ratio and proportion have their applications in solving many day-to-day problems, like when we compare heights, weights, distance or time or while adding ingredients in cooking, and so on.
| 1. | What is Ratio and Proportion? |
| 2. | Definition of Ratio |
| 3. | Definition of Proportion |
| 4. | Ratio and Proportion Formula |
| 5. | Difference Between Ratio and Proportion |
| 6. | FAQs on Ratio and Proportion |
What is Ratio and Proportion?
A comparison of two quantities by division is called a ratio and the equality of two ratios is called proportion. A ratio can be written in different forms like x : y or x/y and is commonly read as, x is to y.
On the other hand, proportion is an equation that says that two ratios are equivalent. A proportion is written as x : y : : z : w, and is read as x is to y as z is to w. Here, x/y = z/w where w & y are not equal to 0.
Definition of Ratio
Ratio is the comparison of two quantities which is obtained by dividing the first quantity by the other. If a and b are two quantities of the same kind and with the same units, such that b is not equal to 0, then the quotient a/b is called the ratio between a and b. Ratios are expressed using the symbol of the colon (:). This means that ratio a/b has no unit and it can be written as a : b
Definition of Proportion
Proportion refers to the equality of two ratios. Two equivalent ratios are always in proportion. Proportions are denoted by the symbol (: :) and they help us to solve for unknown quantities. In other words, proportion is an equation or statement that is used to depict that the two ratios or fractions are equivalent. Four non-zero quantities, a, b, c, d are said to be in proportion if a : b = c : d. Now, let us consider the two ratios - 3 : 5 and 15 : 25. Here, 3 : 5 can be expressed as 3:5 = 3/5 = 0.6 and 15:25 can be expressed as 15:25 = 15/25 = 3/5 = 0.6. Since both the ratios are equal, we can say that these two are proportional.
There are two types of proportions.
- Direct Proportion
- Inverse Proportion
Direct Proportion
Direct proportion describes the direct relationship between two quantities. If one quantity increases, the other quantity also increases and vice-versa. Thus, a direct proportion is written as y ∝ x. For example, if the speed of a car is increased, then it covers more distance in a fixed period of time.
Inverse Proportion
Inverse proportion describes the relationship between two quantities in which if one quantity increases, the other quantity decreases and vice-versa. Thus, an inverse proportion is written as y ∝ 1/x. For example, as the speed of a vehicle is increased, it will cover a fixed distance in less time.
Ratio and Proportion Formula
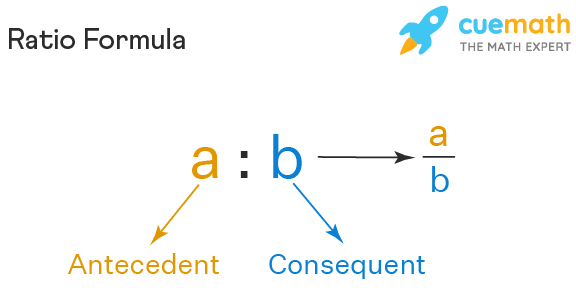
The formula for ratio is expressed as a : b ⇒ a/b, where,
- a = the first term or antecedent.
- b = the second term or consequent.
For example, ratio 2 : 7 is also represented as 2/7, where 2 is the antecedent and 7 is the consequent.
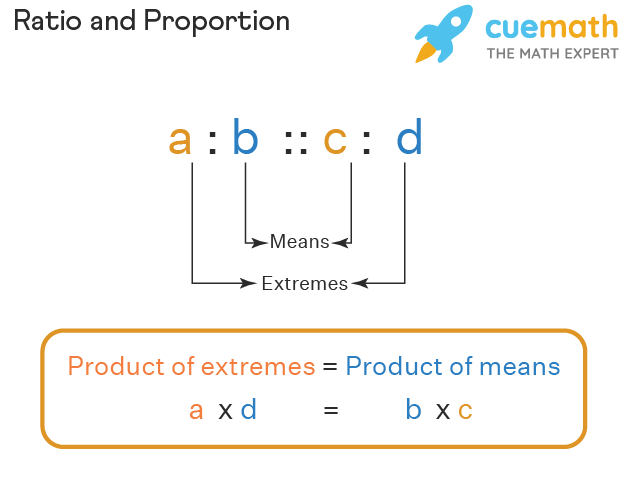
Now, in order to express a proportion for the two ratios, a : b and c : d, we write it as \(a: b:: c: d \longrightarrow \frac{a}{b}=\frac{c}{d}\)
- The two terms b and c are called mean terms.
- The two terms a and d are known as extreme terms.
- In a: b = c : d, the quantities a and b should be of the same kind with the same units, whereas, c and d may be separately of the same kind and of the same units. For example, 5 kg : 15 kg = Rs. 75 : Rs. 225
- The proportion formula can be expressed as, a/b = c/d or a : b : : c : d.
- In a proportion, the product of the means = the product of the extremes. Therefore, in the proportion formula a: b : : c : d, we get b × c = a × d. For example, in 5 : 15 :: 75 : 225, we will get 15 × 75 = 5 × 225
Difference Between Ratio and Proportion
The difference between ratio and proportion can be seen in the following table.
| Ratio | Proportion |
|---|---|
| It is used to compare the size of two quantities with the same unit. | It is used to express the relation of two ratios. |
| The symbols used to express a ratio - a colon (:), slash (/) | The symbol used to express a proportion - double colon (::) |
| It is referred to as an expression. | It is referred to as an equation. |
Important Notes on Ratio and Proportion
- Any two quantities with the same units can be compared.
- Two ratios are said to be in proportion only if they are equal.
- To check whether two ratios are equal and are in proportion, we can also use the cross-product method.
- If we multiply and divide each term of a ratio by the same number, the ratio remains the same.
- For any three quantities, if the ratio between the first and the second is equal to the ratio between the second and the third, then these are said to be in a continued proportion.
- Similarly, in the case of any four quantities in a continued proportion, the ratio between the first and the second is equal to the ratio between the third and the fourth.
Examples on Ratio and Proportion
-
Example 1: Find out if the ratios 6:8 and 24:32 are in proportion.
Solution:
The given ratios are 6:8 and 24:32. 6:8= 3/4 = 0.75 and 24:32 = 3/4= 0.75. Here, both the ratios are equal. Therefore, 6:8 and 24:32 are in proportion.
-
Example 2: There are 30 students in a class. The number of students who like Math and the ones who like Science is expressed in the ratio 2:3. Find the number of students who like Math and the ones who like Science.
Solution:
Total number of students = 30. Let the number of students who like Math = 2x and the number of students who like Science = 3x. We can say that 2x + 3x = 30 ⇒ 5x = 30 ⇒ x = 6. Substituting the value of x = 6, we get the numbers of students who like Math = 2x = 2 × 6 = 12 and the number of students who like Science = 3x = 3 × 6 = 18.
Therefore, 12 students like Math and 18 students like Science.
-
Example 3: State true or false:
a.) Two ratios are said to be in proportion only if they are equivalent.
b.) In the ratio 6 : 8, 6 is the consequent and 8 is the antecedent.
Solution:
a.) True, two ratios are said to be in proportion only if they are equivalent.
b.) False, in the ratio 6 : 8, 6 is the antecedent and 8 is the consequent.

FAQs on Ratio and Proportion
What is Ratio and Proportion?
Ratio is the comparison between the quantities with the same unit. It is obtained by dividing the first quantity by the other. If a and b are two quantities of the same kind and with the same units, such that b is not equal to 0, then the quotient a/b is called the ratio between a and b. On the other hand, proportion is defined to be a comparative relation between two ratios.
What is the Formula of Ratio and Proportion?
The ratio formula for any two quantities is expressed as a : b ⇒ a/b. On the other hand, the proportion formula is expressed as \(a : b : : c : d \longrightarrow \frac{a}{b}=\frac{c}{d}\).
What is the Difference Between Ratio and Proportion?
A ratio depicts a comparison between two quantities whereas proportion depicts the equality of two ratios.
How is Ratio and Proportion used in Real Life?
Ratio and proportion is used in our everyday lives. For example, the food that we eat has a fixed ratio of ingredients. The house or building that we stay in has a fixed ratio and proportion of cement and sand.
How is Ratio and Proportion Related to Each Other?
Ratio and proportion are related to each other. Ratio is used for comparing two quantities of the same kind. When two or more such ratios are equal, they are said to be in proportion.
How is Fraction Related to Ratio and Proportion?
A ratio can also be expressed as a fraction. For example, 1: 3 can also be written as 1/3. When a ratio is written in the fraction form, the fraction needs to be simplified. For example, when the fraction 13/39 is written in the form of a ratio, it will be 1:3. If it is an improper fraction, we do not convert it to a mixed fraction and leave it as an improper fraction because a ratio always compares two quantities.
What are the Two Parts of Proportion?
There are four parts in a proportion but based on their arrangement in the proportion, these are separated into two groups, the means, and the extremes. The outer terms are called extremes and the inner terms are called means. For example, in the proportion, 3 : 4 :: 24 : 32, the numbers 6 and 32 are extremes and 8 and 24 are means.
What is the Difference Between Direct and Inverse Proportion?
In direct proportion, the increase in one quantity leads to the increase in the other or vice versa whereas, in inverse proportion, the increase in one quantity leads to a decrease in the other.
visual curriculum