What is the range of the function g(x) = |x - 12| - 2?

Solution:

Given, the function is g(x) = |x - 12| - 2 -------> (1)

We have to find the range of the function.

The given function is an absolute value function that has a v-shaped graph.

The vertex form of an absolute function is given by

y = a|x - h| + k -------> (2)

Where (h, k) is the vertex

Comparing (1) and (2),

h = 12, k = -2

So, the vertex would be (12, -2).

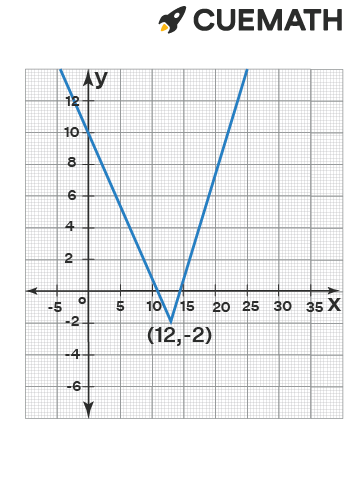
The range of the function is the set of y values for which the function is defined.

The given function has a vertex (12, -2), it would not take any values which are less than -2.

The range would be all y values greater than or equal to -2.

Therefore, the range is given by {y|y ≥ - 2}

---

What is the range of the function g(x) = |x - 12| - 2?

Summary:

The range of the function g(x) = |x - 12| - 2 would be all y values greater than or equal to -2.