A day full of math games & activities. Find one near you.

Homogeneous Differential Equation

A homogeneous differential equation is an equation containing a differentiation and a function, with a set of variables. The function f(x, y) in a homogeneous differential equation is a homogeneous function such that f(λx, λy) = λⁿf(x, y), for any non zero constant λ. The general form of a homogeneous differential equation is f(x, y).dy + g(x, y).dx = 0.

Let us learn more about the homogeneous differential equation, the method to solve a homogeneous differential equation, examples, faqs.

1.	What Is A Homogeneous Differential Equation?
2.	How to Solve a Homogeneous Differential Equation?
3.	Examples on Homogeneous Differential Equation
4.	Practice Questions on Homogeneous Differential Equations
5.	FAQs on Homogeneous Differential Equation

What Is A Homogeneous Differential Equation?

A differential equation containing a homogeneous function is called a homogeneous differential equation. The function f(x, y) is called a homogeneous function if f(λx, λy) = λⁿf(x, y), for any non zero constant λ. The general form of the homogeneous differential equation is of the form f(x, y).dy + g(x, y).dx = 0. The homogeneous differential equation has the same degree for the variables x, y within the equation.

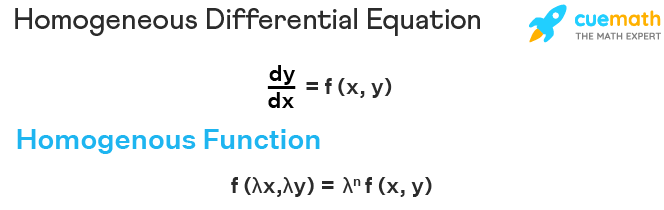
Homogenous Differential Equation

The homogeneous differential equation does not have a constant term within the equation. The linear differential equation has a constant term. The solution of a linear differential equation is possible if we are able to remove the constant term from the linear differential equation and transform it into a homogeneous differential equation. Also, the homogeneous differential equation does not have the variables x, y within any special functions such as logarithmic, or trigonometric functions.

Examples of Homogeneous Differential equations.

dy/dx = (x + y)/(x - y)
dy/dx = x(x - y)/y²
dy/dx = (x² + y²)/xy
dy/dx = (3x + y)/(x - y)
dy/dx = (x³ + y³)/(xy² + yx²)

In these above examples, we can substitute x = λx, and y = λy, to prove it for the homogeneous differential equation. Also, if the homogeneous differential equation is of the form dx/dy = f(x, y), and f(x, y) is a homogeneous function, then we substitute x/y = v, or x = vy. This on further integration, and substituting back the variables x, y, gives the general solution of the homogeneous differential equation.

How To Solve a Homogeneous Differential Equation?

The general solution of the homogeneous differential equation can be obtained by the integration of the given differential equation. A homogeneous differential equation of the form dy/dx = f(x, y), is solved by first separating the variable and the derivative of the particular variable on either side and then integrating it with respect to the variable.

To solve a homogeneous differential equation of the form dy/dx = f(x, y), we make the substitution y = v.x. Here it is easy to integrate and solve with this substitution. Further the differentiation of y = vx, with respect to x we get dy/dx = v + x.dv/dx. We can substitute the value of dy/dx in the expression dy/dx = f(x, y) = g(y/x) to get the below expression.

v + x.dv/dx = g(v)

xdv/dx = g(v) - v

Separating the variables x and v, we have:

\(\dfrac{dv}{g(v) - v} = \dfrac{dx}{x}\)

Here we integrate it on both sides, which results in the following expression.

\(\int \dfrac{1}{g(v) - v}.dv = \int \dfrac{1}{x}.dx\)

The above expression gives the following solution, which is the general solution of the differential equation.

\(\int \dfrac{1}{g(v) - v}.dv = Logx + C\)

Here we substitute back the value of v = y/x, to obtain the general solution of the homogeneous differential equation. The presence of +C in the solution, refers it as a general solution, and further solving and substituting the value of +C, we can obtain the particular solution of the given homogeneous differential equation.

Related Topics

The following topics help in a better understanding of the homogeneous differential equations.

Examples on Homogeneous Differential Equation

Example 1: Show that the differential equation (x - y).dy/dx = (x + 2y) is a homogeneous differential equation.

Solution:

(x - y).dy/dx = (x + 2y) is the given differential equation.

To prove that the above differential equation is a homogeneous differential equation, let us substitute x = λx, and y = λy.

Here we have F(x, y) = \(\dfrac{(x + 2y)}{(x - y)}\)

F(λx, λy) = \(\dfrac{(λx + 2λy)}{(λx - λy)}\)

F(λx, λy) = \(\dfrac{λ(x + 2y)}{λ(x - y)}\) = λ⁰f(x, y)

Therefore, the given differential equation is a homogeneous differential equation.
Example 2: Find the solution of the homogeneous differential equation xCos(y/x).dy/dx = yCos(y/x) + x.

Solution:

The given differential equation is xCos(y/x).dy/dx = yCos(y/x) + x

dy/dx = \(\dfrac{yCos(y/x) + x}{xCos(y/x)}\)

dy/dx = \(\dfrac{x((y/x).Cos(y/x) + 1)}{xCos(y/x)}\)

dy/dx = \(\dfrac{((y/x).Cos(y/x) + 1)}{Cos(y/x)}\)

Here let us substitute y/x =v in the above expression.

dy/dx = \(\dfrac{vCosv + 1}{Cosv}\)

Here we write y/x = v as y = vx. Differentiating y = vx on both sides we obtain dy/dx = v + x.dv/dx, which is substituted in the above expression.

v + x.dv/dx = \(\dfrac{vCosv + 1}{Cosv}\)

x.dv/dx = \(\dfrac{vCosv + 1}{Cosv}\) - v

Here we separate the variables on either side of the equal to symbol.

x.dv/dx = 1/Cosv

Cosv.dv = dx/x

Integrating this expression on both sides, we have the below expression.

\(\int Cosv.dv = \int \dfrac{1}{x}.dx\)

Sinv = Logx + C

Here we substitute back y/x = v.

Sin y/x = Logx + C

Therefore, the solution of the homogeneous differential equation is Sin y/x = Logx + C.

go to slide go to slide

Have questions on basic mathematical concepts?

Become a problem-solving champ using logic, not rules. Learn the why behind math with our certified experts

Book a Free Trial Class

Practice Questions on Homogeneous Differential Equations

go to slide go to slide

FAQs on Homogeneous Differential Equation

What Is Homogeneous Differential Equation?

The homogeneous differential equation containing is a differential equation containing a homogeneous function. The homogeneous differential equation of the form dy/dx = f(x, y), has a homogeneous function f(x, y) such that f(λx, λy) = λⁿf(x, y), for any non zero constant λ. The general form of the homogeneous differential equation is of the form f(x, y).dy + g(x, y).dx = 0.

What Is the Difference Between Homogeneous and Non-Homogeneous Differential Equation?

The homogeneous differential equation consists of a homogeneous function f(x, y), such that f(λx, λy) = λⁿf(x, y), for any non zero constant λ. A non-homogeneous differential equation does not contain a homogeneous function. The example of a non homogeneous differential equation is a linear differential equation of the form dy/dx + Py = Q.

What Are the Examples of Homogeneous Differential Equation?

A few of the examples of homogeneous differential equations are as follows.

dy/dx = (x + y)/(x - y)
dy/dx = (x² + y²)/xy
dy/dx = (3x + y)/(x - y)
dy/dx = (x³ + y³)/(xy² + yx²)

What Is the Formula for Homogeneous Differential Equation?

The general form of a homogeneous differential equation is f(x, y).dy + g(x, y).dx = 0. Here the function f(x, y) is a homogeneous function such that f(λx, λy) = λⁿf(x, y), for any non zero constant λ. Also, there is no defined formula for a homogeneous differential equation, or to find the solution of it. The homogeneous differential equation is solved through a sequence of steps.

What Are the Steps to Solve Homogeneous Differential Equation?

The homogeneous differential equation of the form dy/dx = f(x, y), can be solved through the following sequence of steps.

Step - 1: Substitute y = vx in the given differential equation.
Step - 2: Separate the variables and the differentiation of the variables on either side of the equals to symbol.
Step - 3: Find the integration of the variables and to find the general solution containing v and x.
Step - 4: Substitute back the value of v to get the general solution in the variables x and y.

Math worksheets and
visual curriculum