Linear Differential Equation

Linear differential equation is an equation having a variable, a derivative of this variable, and a few other functions. The standard form of a linear differential equation is dy/dx + Py = Q, and it contains the variable y, and its derivatives. The P and Q in this differential equation are either numeric constants or functions of x.

The linear differential equation in an important form of a differential equation and can be solved using a formula. Let us learn the formula and derivation, to find the general solution of a linear differential equation.

The linear differential equation is of the form dy/dx + Py = Q, where P and Q are numeric constants or functions in x. It consists of a y and a derivative of y. The differential is a first-order differentiation and is called the first-order linear differential equation.

This linear differential equation is in y. Similarly, we can write the linear differential equation in x also. The linear differential equation in x is dx/dy + \(P_1\)x = \(Q_1\).

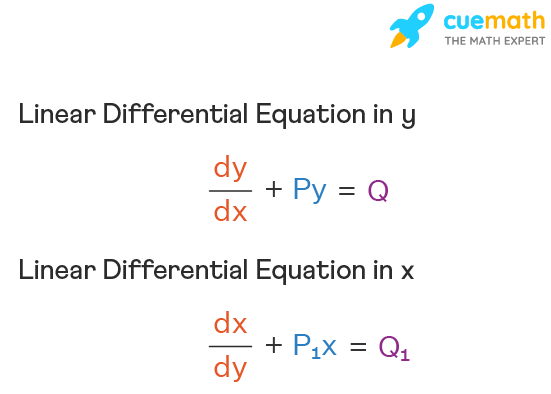
Some of the examples of linear differential equation in y are dy/dx + y = Cosx, dy/dx + (-2y)/x = x².e^-x. And the examples of linear differential equation in x are dx/dy + x = Siny, dx/dy + x/y = ey. dx/dy + x/(ylogy) = 1/y.

The derivation for the general solution for the linear differential equation can be understood through the below sequence of steps. The first-order differential equation is of the form.

dy/dx +Px = Q

Here we multiply both sides of the equation by a function of x, say g(x) . Further, this function is chosen such that the right hand side of the equation is derivative of y.g(x). d/dx(y.g(x)) = y.g(x).

g(x).dy/dx + P.g(x).y = Q.g(x)

Choose g(x) in such a way such that the RHS becomes the derivative of y.g(x).

g(x).dy/dx + P.g(x)y = d/dx(y.g(x)]

The right hand side of the above expression is derived using the derivative formula for the product of functions.

g(x).dy/dx + P.g(x).y = g(x).dy/dx + y.g'(x)

P.g(x) = g'(x)

P = g'(x)/g(x)

Integrating both sides with respect to x, we get

\(\int P.dx= \int \frac{g'(x)}{g(x)}.dx\)

\(\int P.dx= log(g(x))\)

\(g(x)= e^{\int P.dx}\)

This function \(g(x)= e^{\int P.dx}\) is called the Integrating Factor (I.F) of the given linear differential equation. Substituting the value of g(x) in equation linear differential equation, the following expression is obtained.

\(e^{\int P.dx}.\dfrac{dy}{dx} + Pe^{\int P.dx}y = Q.e^{\int P.dx}\)

\(\dfrac{d}{dx}(y.e^{\int P.dx} )= Qe^{\int P.dx}\)

Integrating both sides, with respect to x the following expression is obtained..

\(y.e^{\int P.dx} =\int (Q.e^{\int P.dx}.dx)\)

\(y=e^{-\int P.dx} .\int (Q.e^{\int P.dx}.dx) + C\)

The above expression is the general solution of the linear differential eqution.

The following are the two important formulas to find the general solution of the linear differential equations.

1. The general solution of the differential equation dy/x +Py = Q is as follows. \(y.(I.F)=\int (Q.(I.F).dx)+ C\). Here we have Integrating Factor (I.F) = \(e^{\int P.dx}\).
2. Also the general solution of the differential equation dx/y +Px = Q is as follows. \(x.(I.F)=\int (Q.(I.F).dy)+ C\). Here we have Integrating Factor (I.F) = \(e^{\int P.dy}\).

The following three simple steps are helpful to write the general solutions of a linear differential equation.

• Step - I: Simplify and write the given differential equation in the form dy/dx + Py = Q, where P and Q are numeric constants or functions in x.
• Step - II: Find the Integrating Factor of the linear differential equation (IF) = \(e^{\int P.dx}\).
• Step-III: Now we can write the solution of the linear differential equation as follows. \(y(I.F) = \int(Q × I.F).dx + C\)

The usage of the above steps can be more clearly understood through the below-solved examples of the linear differential equation.

Related Topics

• Calculus
• Integration Formulas
• Differentiation and Integration Formulas
• Chain Rule Formula
• Differential Equations

What Is a Linear Differential Equation?

The linear differential equation is an equation having a variable, a derivative of this variable, and a few other functions. The standard form of a linear differential equation is dy/dx + Py = Q, and it contains the variable y, and its derivatives. The P and Q in this differential equation are either numeric constants or functions of x.

How Do You Know If a Differential Equation Is a Linear Differential Equation?

A differential equation is said to be a linear differential equation if it has a variable and its first derivative. The linear differential equation in y is of the form dy/dx + Py = Q, Here we have the variable y, the first derivative of the variable y, and we have P, Q which are functions in x. From the name of linear, these differential equations have only the first degree derivatives.

How Do You Solve a Linear Differential Equation?

The solution of a linear differential equation is through three simple steps. First simplify and write the given differential equation in the form dy/dx + Py = Q. For this find the Integrating Factor (IF) = \(e^{\int P.dx}\). Finally the solution of the linear differential equation is \(y(I.F) = \int(Q × I.F).dx + C\)

What Is the Standard Form of Linear Differential Equation in x?

The standard form of the linear differential equation in x is dx/dy + Px = Q, This is a differential equation having a variable x, the first derivative of x, and P, Q represent the functions in y. The linear differential equation in x has first-order derivative of x.

What Is the Formula For the General Solution of Linear Differential Equation

The formula for general solution of the differential equation dy/x +Py = Q is \(y.(I.F)=\int (Q.(I.F).dx)+ C\). Here we have Integrating Factor (I.F) = \(e^{\int P.dx}\). Also the formula for the general solution of the differential equation dx/y +Px = Q is \(x.(I.F)=\int (Q.(I.F).dy)+ C\). Here we have Integrating Factor (I.F) = \(e^{\int P.dy}\).