Compound Interest Half Yearly Formula
The compound interest half-yearly formula helps in calculating the value by dividing the rate by 2 and multiplying the time by 2. Compound interest is the interest paid on both principal and interest, compounded at regular intervals where the new principal is calculated. The new principal is equal to the sum of the Initial principal, and the interest accumulated so far. Let us learn more about the compound interest half-yearly formula, the derivations, and solve a few examples.
What is the Compound Interest Half Yearly Formula?
The interest in the case of compound interest varies based on the period of computation. If the time period for the calculation of interest is half-yearly, the interest is calculated every six months, and the amount is compounded twice a year. The compound interest half-yearly formula makes the number of years double and the rate of interest is made into half. The formula to calculate the compound interest when the principal is compounded semi-annually or half-yearly is given as:

Here the compound interest is calculated for the half-yearly period, and hence the rate of interest r, is divided by 2 and the time period is doubled. The formula to calculate the amount when the principal is compounded semi-annually or half-yearly is given by:
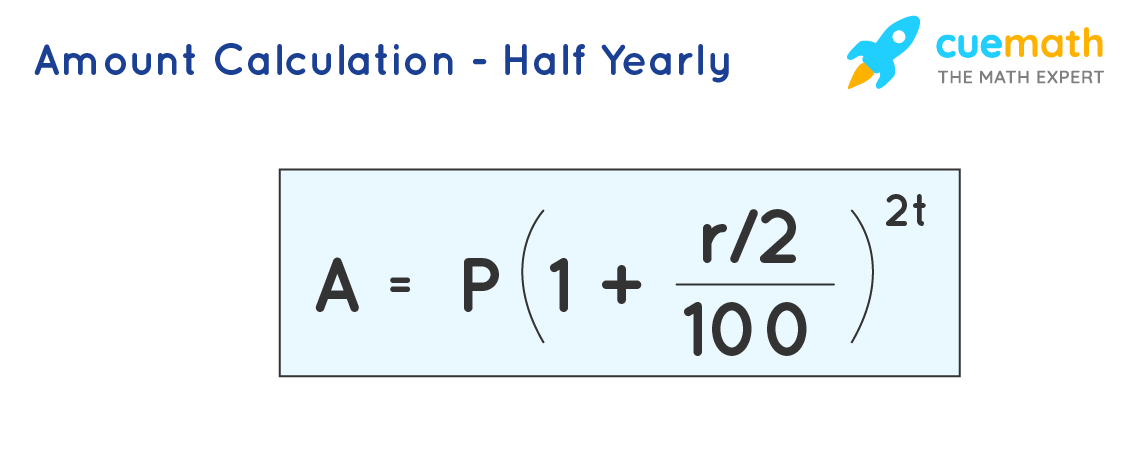
In the above expression,
- A is the amount at the end of the time period
- P is the initial principal value, r is the rate of interest per annum
- t is the time period
- C.I. is the compound interest.
Compound Interest Formula
The compound interest is calculated, after calculating the total amount over a period of time, based on the rate of interest, and the initial principal. For an initial principal of P, rate of interest per annum of r, time period t in years, frequency of the number of times the interest is compounded annually n, the formula for calculation of amount is as follows.

In the above expression,
- P is the principal amount
- r is the rate of interest(decimal)
- n is frequency or no. of times the interest is compounded annually
- t is the overall tenure.
Derivation of Compound Interest Half Yearly Formula
While deriving the formula, we consider the compound interest half-yearly on a principal P kept for 1 year at interest rate r % compounded half-yearly. The principal amount will change at the end of the first 6 months as the interest is compounded half-yearly. The interest for the next six months will be calculated on the amount remaining after the first six months. Simple interest at the end of the first six months,
SI1 = (P × r × 1)/(100 × 2)
Amount at the end of the first six months,
A1 = P + SI1
A1 = P + (P × r × 1)/(2 × 100)
A1 = P[1 + r/(2 × 100)]
A1 = P2
Simple interest for the next six months, now the principal amount has changed to P2
SI2 = (P2 × r × 1)/(100 × 2)
Amount at the end of 1 year,
A2 = P2 + SI2
A2 = P2 + (P2 × r × 1)/(2 × 100)
A2 = P2[1 + r/(2 × 100)]
A2 = P(1 + r/2×100)(1 + r/2×100)
A2 = P[1 + r/(2 × 100)]2
Now we have the final amount at the end of 1 year:
A = P[1 + r/(2 × 100)]2
Rearranging the above equation,
A = P[1 + (r/2)/100)2×1×t

Examples on Compound Interest Half-Yearly Formula
Example 1: Solve the above-given problem using the compound interest formula.
Solution:
The principal amount 'P' is $6000. The rate of interest 'r' is 10% per annum. Conversion period = Half-year, Rate of interest per half-year = 10/2% = 5%. The time period 't' is 2 years. The compounding frequency 'n' is 2.
Let us substitute the given data in the compound interest formula: A = P(1+{r / 2}/100)2t= 6000(1+{10 / 2}/100)2(2)= $6862.03
Therefore the final amount is $6862.03, and the compound interest formula makes the solution simple.
Example 2: Find the compound interest on $3000 for 3/2 years at 10% per annum, interest is payable half-yearly?
Solution: Given,
A = $3000
2t = 2×3/2 = 3
r = 10%
Therefore, substituting the values in the compound interest half-yearly formula,
A = P(1+{r / 2}/100)2t = 3000(1 + {10/2}/100)3 = 3472.88
CI = A - P
CI = 3472.88 - 3000
CI = 1.16.
Therefore, the compound interest is 3472.88.
FAQs on Compound Interest Half Yearly Formula
What is the Formula to Calculate the Compound Interest Half Yearly?
The formula to calculate the compound interest is:
CI = [P(1+{r / 2}/100)2t] - P
Where,
- A is the amount at the end of the time period
- P is the initial principal value, r is the rate of interest per annum
- t is the time period
- C.I. is the compound interest.
What is the Monthly Compound Interest Formula?
The monthly compound interest formula is given as
CI = P(1 + (r/12) )12t - P. Where, P is the principal amount, r is the interest rate in decimal form, n = 12 (it means that the amount compounded 12 times in a year), and t is the time.
What is the Daily Compound Interest Formula?
The daily compound interest formula is given as
A = P (1 + r / 365)365 t, where P is the principal amount, r is the interest rate of interest in decimal form, n = 365 (it means that the amount compounded 365 times in a year), and t is the time.
Can Compound Interest be Greater than Principal?
The compound interest can be greater than the principal. The compound interest value varies and increases for successive time periods. An initial principal of $100 invested over a period of time would give a compound interest of $10, $11, $12.1, $13.31....over successive time periods of 1 year each. Thus the compound interest increases over a period of time and can be greater than the initial principal value.
How Do you Calculate Compound Interest for Half Year?
The formula for calculation of compound interest for half year is CI = p(1 + {r/2}/100)2t.- p. Here in this formula 'A' is the final amount, 'p' is the principal, and 't' is the time in years. In the formula, we can observe that the rate of interest is halved and the time is doubled, to account for the calculation of compound interest for half a year.
visual curriculum