Formula for Finding Angles
Before learning the formulas for finding angles, let us see the situations where we may need to use these formulas. There are different formulas for finding angles depending on the available data. Let us learn the formulas of finding angles case by case here.
- To find the missing angle in a polygon, we use the sum of interior angles formula.
- To find the missing angle in a right-angled triangle, we use trigonometric ratios.
- To find the missing angles in a non-right-angled triangle, we use the law of sines and the law of cosines.
What Is Formula for Finding Angles?
Here are the formulas for finding angles. We choose one of these formulas to find the unknown angles depending on the given information.
|
Formula name |
Formula | How to find unknown angles? |
|---|---|---|
|
180 (n-2) degrees |
Find the sum of all interior angles using this formula and subtract the sum of all known angles from this to find the unknown interior angle. | |
| sin, cos, and tan |
sin θ = opposite / hypotenuse |
Use one of these trigonometric ratios depending on what two sides are available to find the unknown angle. |
| Law of sines |
a/sin A = b/sin B = c/sin C Here, A, B, and C are the angles of a triangle and a, b, and c are their respective opposite sides. |
The law of sines is be used to find unknown angles when we are given with a) two sides and a non-included angle (or) b) two angles and a non-included side. |
| Law of cosines |
a2 = b2 + c2 - 2bc cos A Here, A, B, and C are the angles of a triangle and a, b, and c are their respective opposite sides. |
The law of cosines is used to find unknown angles when we are given with a) three sides (or) b) two sides and the included angle. |

Examples Using Formula for Finding Angles
Example 1: Find the fifth interior angle of a pentagon if four of its interior angles are 108°, 120°, 143°, and 97°.
Solution:
The number of sides of a pentagon is, n = 5.
The sum of all 5 interior angles of a pentagon = 180 (n -2)° = 180 (5 - 2)° = 540°.
The sum of the given 4 interior angles = 108°+ 120°+ 143°+ and 97°= 468°.
So the fifth interior angle = 540° - 468° = 72°.
Answer: The fifth interior angle of the given pentagon = 72°.
Example 2: Find the angle at the vertex C in the following triangle using one of the formulas for finding angles. Round your answer to the nearest integer.

Solution:
To find: The angle at C which is θ.
It is given that AB = 6 = Opposite side of θ.
BC = 8 = Adjacent side of θ.
Since we know both opposite and adjacent sides of θ, we use tan θ formula to find θ.
tan θ = opposite/adjacent
tan θ = 6/8 = 0.75
θ = tan-1 (0.75)
Using the calculator,
θ ≈ 37° (Rounded to the nearest integer).
Answer: The angle at C is, θ = 37°
Example 3: Find the angle at vertex A in the following triangle using one of the formulas for finding angles. Round your answer to the nearest tenths.
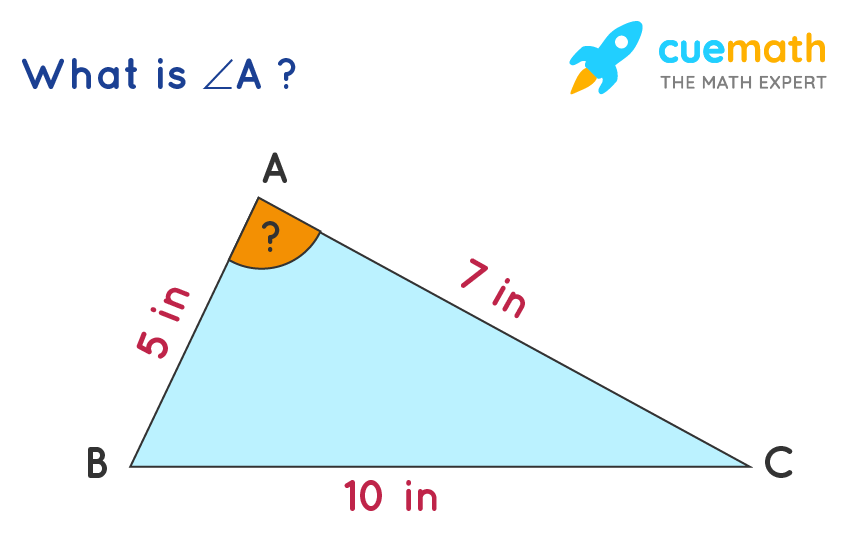
Solution:
To find: The angle at A.
We know that the sides opposite to A, B, and C are represented by a, b, and c respectively. So we have:
a = 10 in; b = 7 in; and c = 5 in.
Since we know all three sides, we have to use the law of cosines to find the angle at A.
a2 = b2 + c2 - 2bc cos A
102 = 72 + 52 - 2 (7)(5) cos A
100 = 49 + 25 - 70 cos A
100 = 74 - 70 cos A
70 cos A = 74 - 100
70 cos A = -26
cos A = -26 / 70
A = cos-1 (-26/70)
Using the calculator,
A ≈ 111.8° (Rounded to the nearest tenths).
Answer: The angle at A = 111.8°
visual curriculum