There has been a growing need for a focused and coherent mathematics curriculum in the United States to improve achievement in mathematics. To address this need, the United States Common Core Standards (USCC) for mathematics for each grade have been laid out. The standards are described in detail to help educators plan appropriate pedagogical approaches to ensure achievement of outcomes. These standards are drawn in from research in math education and models of best mathematical practices across the world.

Here are the highlights of the grade specific standards.

GRADE 1
In Grade 1, building number sense is given utmost importance. Mentally adding and subtracting numbers up to 20, understanding the place value of 2-digit numbers, and Adding and Subtracting numbers up to 100 using place value are some of the key areas of focus under number sense. In addition to numbers, the idea of units to measure length, intuitive understanding of data and basic attributes of 2D and 3D shapes are also dealt with.

In order to facilitate mastery of abstract concepts by young learners, Cuemath adopts a Concrete-Pictoria-Abstract (CPA) approach. The curriculum is aided with concrete models and visuals as much as possible to make the transition from concrete to abstract concepts seamless.

The curriculum for grade 1 spreads across four major domains.

1. Operations in Algebraic Thinking
2. Numbers and Operations in Base Ten
3. Measurement and Data
4. Geometry

Operations in Algebraic Thinking

USCC standards focus on algebraic thinking from early years to ensure easy transition from arithmetic to algebra in middle school. Children often struggle to frame algebraic expressions or equations when they start learning algebra. This can be attributed to difficulty in understanding word problems and translating them to mathematical statements. The examples of word problems that are commonly seen in textbooks are those of putting together two groups in case of addition or taking away objects from a group in case of subtraction. There is also an undue emphasis on ‘keywords’ such as ‘together’ or ‘total’ for addition and ‘left’ or ‘remaining’ for subtraction.

To address these issues, common core standards recommend exposure to a wide range of situations on addition and subtraction such as increase in a quantity for addition and partitioning a group of objects into two or more parts and comparison between two quantities in case of subtraction. It recommends representation of these situations using visual models for better comprehension. Taking these recommendations into consideration, the Cuemath curriculum provides experience of different types of situations to help students understand the meaning of these operations. 

One such example of a word problem on subtraction is shown below.

In the above example, children can visualize subtraction as ‘counting on’ from the smaller number (3) to the larger number (7). Through such examples they also realize that subtraction not only means taking away but it can also be used to compare two quantities. They also learn to formulate mathematical statements from a variety of situations.

Numbers and Operations in Base Ten

Numbers are fundamental to mathematics. However, in traditional teaching, children are made to recite numbers from 1 to 100 without understanding what these numbers mean. Since the initial understanding of children is concrete and pictorial, it is important to help them understand how a number is composed of tens and ones using base ten blocks (flats rods and blocks). USCC standards recommend the introduction of tens as bundles of ones to understand the number structure. This helps them understand the place value system.
Here is an example from the Cuemath curriculum on visual models to represent numbers by base ten blocks. An orange block represents a ‘one’ and a blue rod represents a ‘ten’.

Through examples as shown above, children can understand that the value of the digit ‘2’ in the number 42 is 2 ones while the value of the same digit in 27 is 2 tens or twenty. 

USCC standards further recommend addition and subtraction of numbers within 100 using these visual models. Children usually find addition or subtraction that involve regrouping quite difficult. However, if they can visualize the process of addition using models, such difficulties can be largely minimized.
The simulation from the Cuemath Curriculum below shows how these models can be used to understand the process of addition of 37 and 15.

Here, children can observe that 7 ones from 37 and 5 ones from 15 combine to form 12 ones. But, 12 ones can be regrouped to form 1 ten and 2 ones and hence the sum would be 52. Once this understanding is built, children will be able to relate this with the standard algorithm of addition.

Measurement and Data 
Let us look at this question that asks to find the length of a pencil using a broken ruler. 

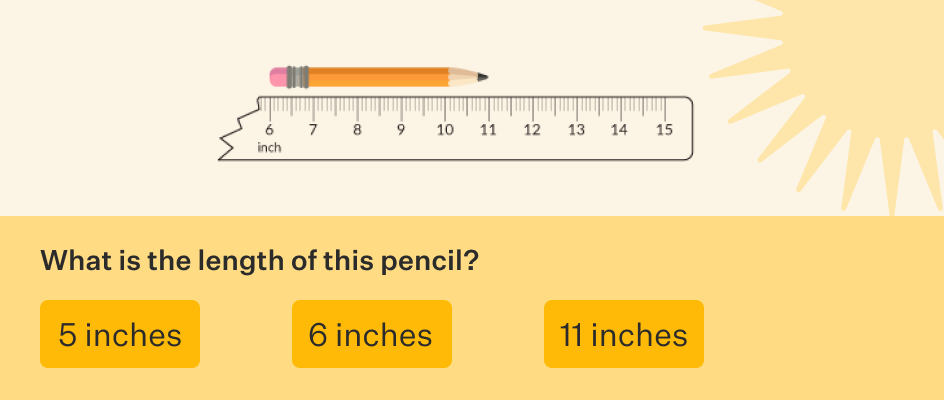
The obvious answer for us is 5 inches. However, many children would select the length of the pencil as 6 inches or 11 inches.
A probable reason for selecting the length of the pencil as 6 inches could be counting the number of inch marks on the ruler from the end to the tip of the pencil.On the other hand, a probable reason for selecting the length of the pencil as 11 inches could be that the tip of the pencil coincides with the 11 inch mark on the ruler. Both the cases indicate gaps in understanding how to use units to measure length.

In order to address these misconceptions, USCC standards recommend tasks to help children understand three important characteristics of units to measure length.

1. They should be of the same size.
2. They should be placed in a manner that there are no gaps and overlaps.
3. The length of the object being measured would be the number of iterations of the unit.

The following example from the Cuemath curriculum shows how the idea of units is developed by measuring the length of an object by placing smaller objects of the same size along the length of the object.

With tasks such as above, students will eventually understand how many units for measuring length are used.
In addition to measurement of length, USCC also lays the foundation of data analysis quite early. The standards focus on engaging tasks such as categorizing objects in groups, counting and comparing the number of objects in different groups.

Geometry
If we look at the two figures given below, which one would be easier for a 7 or 8 year old child to identify as a square?

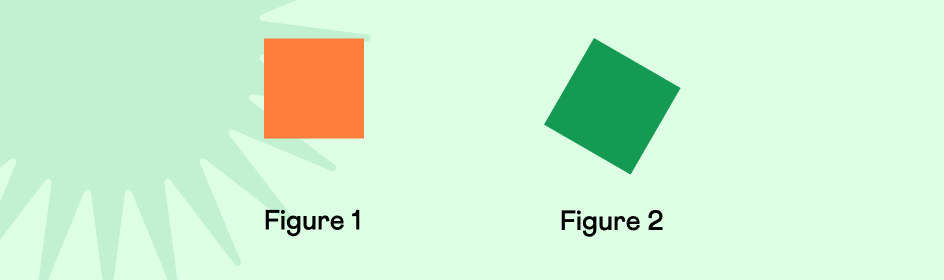
Isn’t it relatively easy to identify Figure 1 as a square? Square in a different orientation in Figure 2 makes it slightly challenging to identify. 
This happens because often 2D or 3D shapes are introduced either in horizontal or vertical orientation. Thus, a prototype of the shape is generated in the minds of children. They begin to believe that orientation is one of the defining attributes of a shape. However, as educators, we should always challenge this thinking by giving examples of shapes in different sizes, colors and orientations to help children understand that these attributes do not define a shape as shown in the task above.
In the above task, the two squares are of different colours, size and orientation. Identifying them from a given set of shapes will indicate that the child has understood the attributes of a square.
 ‘Reasoning with shapes and attributes’ is one of the major standards in geometry and it emphasizes distinction between defining attributes (example: triangles are closed and made up of 3-sides) and non-defining attributes (size, color and orientation) of 2D and 3D shapes.
With this basic understanding of shapes it further suggests tasks to create new shapes using known shapes and also partitioning shapes into halves and quarters.

A good foundation of mathematics in early years goes a long way in developing mathematical thinking in later years. Hence, in Grade 1, the Cuemath curriculum provides learning experiences of important concepts through concrete and pictorial representations and connects mathematics with the lives of students. Cuemath conducts Live Online Math classes. This makes them love math and see its relevance in their day to day lives. It is expected that with this experience they will be confident to learn these concepts in more detail in Grade 2.

-By Joyita Banerjee

Joyita heads the curriculum for K-6 and assessments at Cuemath. She has a Master's degree in education and a Post-graduate diploma in Information Technology. With over 15 years of experience, she has expertise in designing and developing curriculum for students and training teachers in math education and educational assessments. Her passion lies in helping children from different social classes master math concepts. In her free time, she loves reading, listening to music and spending time with her family.