Area of Isosceles Triangle

The area of an isosceles triangle is the amount of space enclosed between the sides of the triangle. Besides the general area of the isosceles triangle formula, which is equal to half the product of the base and height of the triangle, different formulas are used to calculate the area of triangles, depending upon their classification based on sides. These different types based on sides are given below:

• Equilateral Triangle- A triangle with all sides equal.
• Isosceles Triangle- A triangle with any two sides/angles equal.
• Scalene Triangle- A triangle with all unequal sides.

Let us understand the area of the isosceles triangle in detail in the following section.

The area of an isosceles triangle is the total space or region covered between the sides of an isosceles triangle in two-dimensional space. An isosceles triangle is defined as a triangle having two sides equal, which also means two equal angles. Here are some properties of an Isosceles triangle that distinguish it from other types of triangles:

• The two equal sides of an isosceles triangle are called the legs and the angle between them is called the vertex angle or apex angle.
• The side opposite the vertex angle is called the base and base angles are equal.
• The perpendicular from the vertex angle bisects the base and it also bisects the vertex angle.

The area of an isosceles triangle is expressed in square units. Therefore, some units that can be used to represent the area of an isosceles triangle are m², cm², in², yd², etc.

The area of an isosceles triangle refers to the total space covered by the shape in 2-D. The area of an isosceles triangle can be calculated in many ways based on the known elements of the isosceles triangle. The general basic formula that can be used to calculate the area of an isosceles triangle using height is given as, (1/2) × Base × Height

The following table summarizes different formulas that can be used to calculate the area of an isosceles triangle, for a different set of known parameters.

where,

• b = base of the isosceles triangle
• a = measure of equal sides of the isosceles triangle
• α = measure of equal angles of the isosceles triangle
• β = measure of the angle opposite to the base

If the length of the equal sides and the base of an isosceles triangle are known, then the height or altitude of the triangle can be calculated. The formula to calculate the area of an Isosceles triangle using sides is given as,

Area of isosceles triangle using only sides = ½[√(a² - b²/4) × b]

where,

• b = base of the isosceles triangle
• h = height of the isosceles triangle
• a = length of the two equal sides

Derivation:

From the above figure, we know:

BD = DC = ½ BC = ½ b (perpendicular from the vertex angle bisects the base)
AB = AC = a (equal sides of an isosceles triangle)

Applying Pythagoras' theorem for ΔABD, we get:
a² = (b/2)² + (AD)²
AD = √(a² − b²/4)

The altitude of an isosceles triangle = √(a² − b²/4)

Also, we know the general area of the triangle formula is given as:
Area = ½ × b × h

Substituting value for height:

Area of isosceles triangle using only sides = ½[√(a² − b² /4) × b]

The area of an isosceles triangle formula can be easily derived using Heron’s formula as explained in the following steps. Heron's formula is used to find the area of a triangle when the measurements of its 3 sides are given.

Derivation:

The Heron's formula to find the area, A of a triangle whose sides are a,b, and c is:

A = √s(s-a)(s-b)(s-c)

where,

• a, b, and c are the sides of the triangle.
• s is the semi perimeter of the triangle.

We know that the perimeter of a triangle with sides a, b, and c is a + b + c. Here, s is half of the perimeter of the triangle, and hence, it is called semi-perimeter.

Thus, the semi-perimeter is:

s = (a + b + c)/2

Now, for an isosceles triangle,

s = ½(a + a + b)

⇒ s = ½(2a + b)

or, s = a + (b/2)

Also,

Area = √[s(s−a)(s−b)(s−c)]

or, Area = √[s (s−a)² (s−b)]

⇒ Area = (s−a) × √[s (s−b)]

Substituting the value for “s”

⇒ Area = (a + b/2 − a) × √[(a + b/2) × ((a + b/2) − b)]

⇒ Area = b/2 × √[(a + b/2) × (a − b/2)]

Area of isosceles triangle = b/2 × √(a² − b²/4) square units

where,

• b = base of the isosceles triangle
• a = length of the two equal sides

The formula to find area of an isosceles triangle using length of 2 sides and angle between them or using 2 angles and length between them can be calculated using basic trigonometry concepts.

Using 2 sides and angle between them:

Area = ½ × b × a × sin(α) square units

where,

• b = base of the isosceles triangle
• a = length of the two equal sides
• α = angle between the unequal sides

Using 2 angles and length between them:

Area = [a² × sin(β/2) × sin(α)] square units

where,

• a = length of the two equal sides
• α, β = angles in an isosceles triangle

A right isosceles triangle is defined as the isosceles triangle which has one angle equal to 90°. The Formula to calculate the area for an isosceles right triangle can be expressed as,

Area = ½ × a²

where a is the length of equal sides.

Derivation:

Let the equal sides of the right isosceles triangle be denoted as "a", as shown in the figure below:

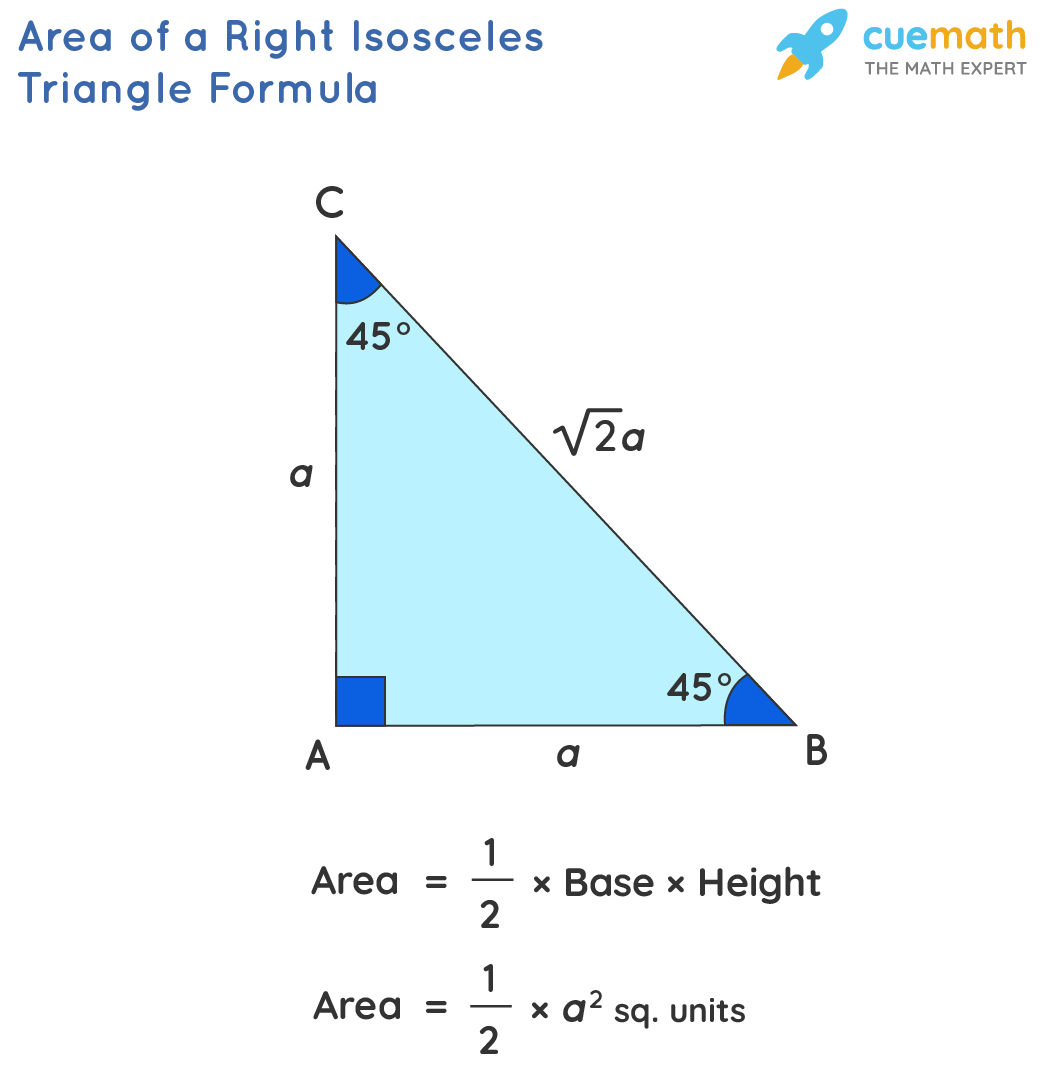
The length of the hypotenuse, BC can be calculated using Pythagoras' Theorem,

BC² = a² + a²

BC = √2 a

Area = ½ × base × height

Area = ½ × a × a = a²/2 square units

What Does the Area of an Isosceles Triangle Mean?

The area of a figure is the region enclosed by the figure. Thus, the area of an isosceles triangle means the total space enclosed by an isosceles triangle.

What is an Isosceles Triangle?

An isosceles triangle is defined as a triangle having two sides equal, which also means two equal angles. Here are some properties of an Isosceles triangle that distinguish it from other types of triangles:

• The two equal sides of an isosceles triangle are called the legs and the angle between them is called the vertex angle or apex angle.
• The side opposite the vertex angle is called the base and base angles are equal.
• The perpendicular from the vertex angle bisects the base and it also bisects the vertex angle.

What is the Formula for Area of Isosceles Triangle?

The area of an isosceles triangle refers to the total space covered by the shape in 2-D. The area of an isosceles triangle can be calculated in many ways based on the known elements of the isosceles triangle.

• Using base and Height: Area = ½ × b × h
• Using all three sides: Area = ½[√(a² − b² ⁄4) × b]
• Using the length of 2 sides and an angle between them: Area = ½ × b × a × sin(α)
• Using two angles and length between them: A = [a²×sin(β/2)×sin(α)]
• Area formula for an isosceles right triangle: Area = ½ × a²

where,

b = base of the isosceles triangle
a = measure of equal sides of the isosceles triangle
α = measure of equal angles of the isosceles triangle
β = measure of the angle opposite to the base

How Do You Find the Height Using Area of an Isosceles Triangle?

The height or altitude of an Isosceles Triangle can be calculated by applying the Pythagorean Theorem for any two sides. The formula to calculate the height of an isosceles triangle is given as,
The altitude of an Isosceles Triangle = √(a² − b²/4) units

where,
b = base of the isosceles triangle
a = measure of equal sides of the isosceles triangle

What is the Perimeter and Area of an Isosceles Triangle?

The perimeter of an isosceles triangle is defined as the length of the boundary of an isosceles triangle. The formula for the perimeter of an isosceles triangle is given as, P = 2a + b units. While area is the total region covered by the isosceles triangle, given as, ½[√(a² − b² ⁄4) × b]
where,

• b = base of the isosceles triangle
• a = measure of equal sides of the isosceles triangle

How Do You Find the Area of an Isosceles Triangle Without Height?

The expression to calculate the area of an isosceles triangle without height can be calculated using Heron's formula. The formula to calculate the area of an isosceles triangle without height is given as,
Area of isosceles triangle = b/2 × √(a² − b²/4)
where,

• b = base of the isosceles triangle
• a = measure of equal sides of the isosceles triangle

How Do You Find the Area of an Isosceles Triangle Given Two Sides and an Angle?

The area of a triangle is half the product of the given two sides and sine of the included angle.
Area of Triangle with 2 Sides and Included Angle (SAS) formula is used to find the general formula for calculating the area of an isosceles triangle for SAS as,
Area = ½ × b × a × sin(α)
where,

• b = base of the isosceles triangle
• a = measure of equal sides of the isosceles triangle
• α = measure of equal angles of the isosceles triangle

How Do You Find the Area of an Isosceles Triangle With 3 Sides?

The area of an isosceles triangle with 3 sides can be calculated using Heron's formula, that is Area = \(\sqrt {s(s - a)(s - b)(s - c)} \). For an isosceles triangle, side c = side a. The general formula to calculate the area of an isosceles triangle is given as,
Area of isosceles triangle = b/2 × √(a² − b²/4)
where,

• b = base of the isosceles triangle
• a = measure of equal sides of the isosceles triangle