Surface Area of Rectangular Prism
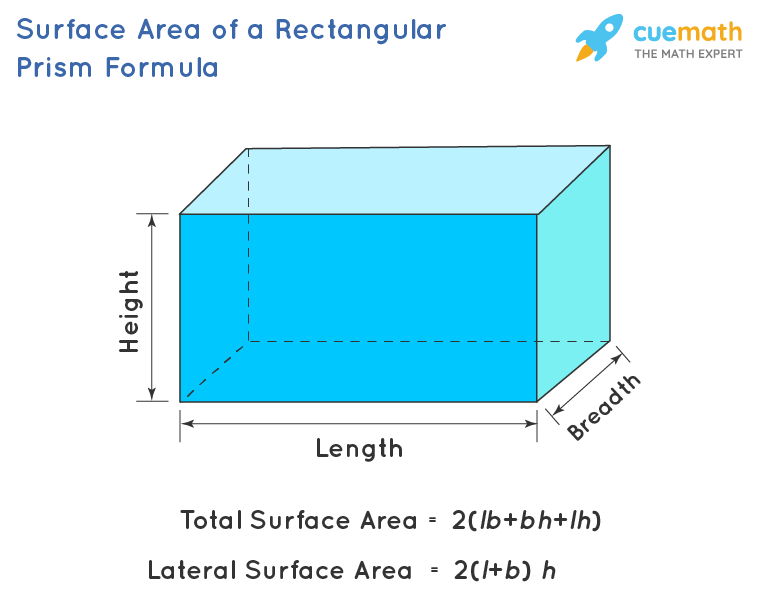
The surface area of a rectangular prism is the total area or region covered by its six faces. If l, b, and h are the length, breadth, and height of a rectangular prism, then:
- Its total surface area (TSA) = 2(lb + bh + lh)
- Its lateral surface area (LSA) = 2h (l + b)
Prisms are solids with flat parallelogram sides and identical polygon bases. There are different types of prisms, namely - triangular prisms, square prisms, rectangular prisms, pentagonal prisms, hexagonal prisms, etc. In this article, you will learn more about the surface area of rectangular prisms.
| 1. | What is Surface Area of a Rectangular Prism? |
| 2. | Surface Area of a Rectangular Prism Formula |
| 3. | How to Find the Surface Area of a Rectangular Prism? |
| 4. | FAQs on Surface Area of a Rectangular Prism |
What is Surface Area of a Rectangular Prism?
The total region or area covered by all the faces of a rectangular prism is defined as the surface area of a rectangular prism. A rectangular prism is a three-dimensional shape. It has six faces, and all the faces are rectangular shaped. Therefore, both the bases of a rectangular prism must also be rectangles. For example, we can relate the surface area of a rectangular prism with the surfaces of the objects given below: a book, a cuboid-shaped aquarium, a box, etc.

For example, let's say there is a box that needs to be gift-wrapped. You need to calculate the amount of wrapping paper that will be needed to cover it. First, you will need to know the sum of the areas of the six surfaces of the box (four lateral side surfaces, top surface, and bottom surface). This total area of the six surfaces is called the surface area of a rectangular prism.
A rectangular prism can be classified as a right rectangular prism or an oblique rectangular prism. In the right rectangular prism, bases are perpendicular to each other whereas, in an oblique rectangular prism, the bases are not aligned one above the other. Let us see the basic formulas to calculate the total surface area and lateral surface area of a rectangular prism in the next section.
Surface Area of Rectangular Prism Formula
To calculate the surface area of a rectangular prism, we need to simply find the sum of the areas of the faces of the prism. A rectangular prism can have two types of areas:
- Total Surface Area (TSA)
- Lateral Surface Area (LSA)
Total Surface Area of Rectangular Prism
The total surface area of a rectangular prism can be calculated by finding the total area of all six faces. The formula to find the surface area of a rectangular prism is given as,
Total surface area of a rectangular prism = 2(lb + bh + lh) square units
where,
- l = Length of the rectangular prism
- b = Breadth of the rectangular prism
- h = Height of the rectangular prism
☛Note: The unit of measurement of the area of the rectangular prism is square units.
Lateral Surface Area of a Rectangular Prism
The lateral surface area of a rectangular prism can be calculated by finding the sum of all the lateral faces of the prism, i.e. the total area excluding the area of the bases. The formula to find the surface area of a rectangular prism is given as,
Lateral surface area of a rectangular prism = 2(l + b) h square units
where,
- l = Length
- b = Breadth
- h = Height of the rectangular prism
Example: Determine the total surface area of a rectangular prism with the following dimensions: Length (l) = 8 inches; Breadth (b) = 5 inches; Height (h) = 7 inches.
Solution: The total surface area of the rectangular prism is given by: 2(lb + bh + lh) = 2(8 × 5 + 5 × 7 + 8 × 7) = 2(40 + 35 + 56) = 2 × 131 = 262 inch2.
How to Find the Surface Area of a Rectangular Prism?
The surface area of a rectangular prism can be calculated using the following steps:
- Step 1: Check if the given dimensions of the rectangular prism are in the same units or not. If not, convert them into the same units.
- Step 2: Once the dimensions are in the same units, understand the need to calculate the lateral surface area or the total surface area according to the given situation.
- Step 3: Implement the formula for lateral surface area 2h(l + b), or total surface area, 2 (lb + bh + lh).
- Step 4: Write the unit as square units along with the values thus obtained.
Now we know the formula and method to calculate the surface area of a rectangular prism, let us now understand how to calculate it with the help of an example.
Example: Determine the minimum area of the wrapping paper required to wrap a rectangular gift box with dimensions as given below:
- Length, l = 24 inches
- Breadth, b = 15 inches
- Height, h = 20 inches
Solution: In this case, we have to find the total surface area of the box. It can be calculated by following the steps given below:
Step 1: Determine the area of the top and bottom faces of the box.
The area of the bottom and the top surfaces are equal, therefore we can simply twice the area of the top or bottom of the box.
2lb = 2 × (24 × 15) = 2 × 360 = 720 inch2
Step 2: Next, we determine the area of the side faces of the box.
2bh = 2 × (15 × 20) = 2 × 300 = 600 inch2
2lh = 2 × (24 × 20) = 2 × 480 = 960 inch2
Step 3: Add the areas of all six faces to determine the total surface area of the box.
2(lb + bh + lh) = 2lb + 2bh + 2lh = 720 + 600 + 960 = 2280 inch2.
Important Notes on Surface Area of Rectangular Prism:
- A rectangular prism with all sides equal is called a cube.
- A rectangular prism in which the faces are not perpendicular to each other is called an oblique rectangular prism.
- If all the edges of a rectangular prism are equal, then the surface area of the prism will be equal to 6 times the area of each face.
- If all the edges of a rectangular prism are equal to 'l', then the volume of the prism is 'l3'.
Surface Area of Rectangular Prism Examples
-
Example 1: Emily needs to buy some cardboard to build a box without a lid 7 feet long, 5 feet wide, and 9 feet high. How much cardboard should she buy?
Solution:
The dimensions of the box are as follows:
Length, l = 7 feet
Breadth, b = 5 feet
Height, h = 9 feet
To find the area of cardboard required, we need to find the total area of the open box. The area of an open box (a box without a lid), can be determined by calculating the total area of 5 surfaces:
- Base area: lb
- Area of 4 lateral faces or lateral surface area: 2(l + b)h = 2lh + 2bh
⇒ Total surface area of the rectangular prism (open box) = lb + 2lh + 2bh
= 7 × 5 + 2 × 7 × 9 + 2 × 5 × 9
= 35 + 126 + 90
= 251 inch2
Answer: ∴ Emily should buy 251 inch2 of cardboard.
-
Example 2: The total surface area of a rectangular prism is 76 ft2 with a base area of 10 ft2 and the perimeter of the base being 14 ft. Determine its height.
Solution:
Let l, b, h be the length, breadth, and height of the rectangular prism respectively.
Base area, lb = 10 ft2
Base perimeter, 2(l + b) = 14 ft
Surface area = 76 ft2Using the surface area of a rectangular prism formula,
Total surface area = 2(lb + bh + lh) = 76 ft2
or, 2lb + 2(l+b)h = 76 ft2
Substituting values, we get,
2 × 10 + 14 × h = 76
20 + 14 × h = 76
14 × h = 56
h = 56/14 = 4 ftAnswer: ∴ The height of the prism is 4 ft.
-
Example 3: If the TSA of a rectangular prism is 382 square units and its LSA is 264 square units, find its base area.
Solution:
We know that the TSA of rectangular prism = 2 (lb + bh + hl) = 382 ⇒ 2lb + 2bh + 2hl = 382...(1)
The LSA of rectangular prism = 2 (bh + hl) = 264 ⇒ 2bh + 2hl = 264... (2)
Subtracting (2) from (1):
2lb = 118
lb = 59
Answer: ∴ The base area of the rectangular prism = 59 square units.

FAQs on Surface Area of Rectangular Prism
What is the Meaning of Surface Area of a Rectangular Prism?
The surface area of a rectangular prism is defined as the area of all the rectangular faces of the prism. It can be of two types: total surface area and lateral surface area.
- The total surface area of a rectangular prism: It refers to the area of all six faces.
- The lateral surface area of a rectangular prism: It covers the area of only the lateral faces and thus doesn't include the base areas.
But in general, just "surface area" refers to the "total surface area" only.
How do you find the Surface Area of a Rectangular Prism?
The surface area of a rectangular prism can be calculated by adding the area of the rectangular faces of the prism. The following steps depict how to find the area,
- Step 1: Note down the dimensions of the rectangular prism and check that they are in the same units.
- Step 2: Apply the formula to calculate the total surface area or the lateral surface area, according to the context of the given question.
TSA of rectangular prism = 2(lb + bh + lh)
LSA of rectangular prism = 2(l + b)h - Step 3: Represent the obtained answer in square units.
What is the Formula for Calculating the Surface Area of a Rectangular Prism?
The formula to calculate the total surface area of a rectangular prism is given as, TSA of rectangular prism = 2(lb + bh + lh), where, l is length, b is breadth and h is the height of the prism. Also, the lateral surface area of a rectangular prism can be calculated using the formula, LSA of rectangular prism = 2(l + b)h square units.
How to Find the Dimensions of a Rectangular Prism With the Surface Area?
We can calculate the missing dimension of a rectangular prism using area by substituting the given values into the formula of the surface area of a rectangular prism, and further solving to obtain the result. The formulas to calculate the surface area of the rectangular prism are given as,
- Total surface area = 2(lb + bh + lh) square units
- Lateral surface area = 2(l + b)h square units
where, l = Length, b = Breadth, and h = Height.
What Happens to the Surface Area of Rectangular Prism When Each of the Dimensions is Doubled?
The surface area of a rectangular prism quadruples when each of the dimensions is doubled. Hence, we obtain a surface area 4 times the original one in this case.
What Unit is Used for Surface Area of Rectangular Prism?
The unit of measurement for the surface area of a rectangular prism is square units or (unit)2. The SI unit is m2, where the other units can be in2, ft2, cm2, etc.
visual curriculum