Rectangular Prism
A rectangular prism is a three-dimensional shape, having six faces, where all the faces (top, bottom, and lateral faces) of the prism are rectangles such that all the pairs of the opposite faces are congruent. Like all three-dimensional shapes, a rectangular prism also has volume and surface area. A rectangular prism is also known as a cuboid. Let us learn more about a rectangular prism along with the formulas to find its volume and surface area.
| 1. | What is a Rectangular Prism? |
| 2. | Rectangular Prism Formulas |
| 3. | FAQs on Rectangular Prism |
What is a Rectangular Prism?
A rectangular prism is a prism whose bases (the top face and the bottom face) are also rectangles. It has 6 faces in all, out of which there are 3 pairs of identical opposite faces, i.e., all the opposite faces are identical in a rectangular prism. It has three dimensions, length, width, and height. Some examples of a rectangular prism in real life are rectangular tissue boxes, school notebooks, laptops, fish tanks, large structures such as cargo containers, rooms, storage sheds, etc. The following figure shows a rectangular prism and its net, which is a two-dimensional representation of the prism when its faces are opened on a 2D plane.
Faces Edges Vertices of a Rectangular Prism
A rectangular prism has 6 faces, 12 edges (sides) and 8 vertices (corners). In the 12 edges, 3 edges intersect to form right angles at each vertex.
Types of Rectangular Prisms
There are two types of rectangular prisms that are classified depending on the shape of the faces or the angle made by the faces with the base.
- Right rectangular prism: In a right rectangular prism, the faces are perpendicular to each of its bases. In this, all side faces are rectangles.
- Oblique rectangular prism: In an oblique rectangular prism, the faces are not perpendicular to the bases. In other words, the faces in this prism are parallelograms.
In general, a rectangular prism without any specifications is a right rectangular prism.
Properties of Rectangular Prism
The properties of a rectangular prism are given below which help us to identify it easily.
- A rectangular prism has 6 faces, 8 vertices, and 12 edges.
- In a right rectangular prism, the faces are rectangles, whereas, in an oblique rectangular prism, the faces are parallelograms.
- It has 3 dimensions which are length, width, and height.
- The opposite faces of a rectangular prism are congruent.
Rectangular Prism Formulas
In this section, we will learn the formulas of the volume and surface area of a rectangular prism. For both of these, let us consider a rectangular prism of length 'l', width 'w', and height 'h'. Along these dimensions, let us assume that 'l' and 'w' are the dimensions of the base. Here are the formulas for the volume and surface area of a rectangular prism.
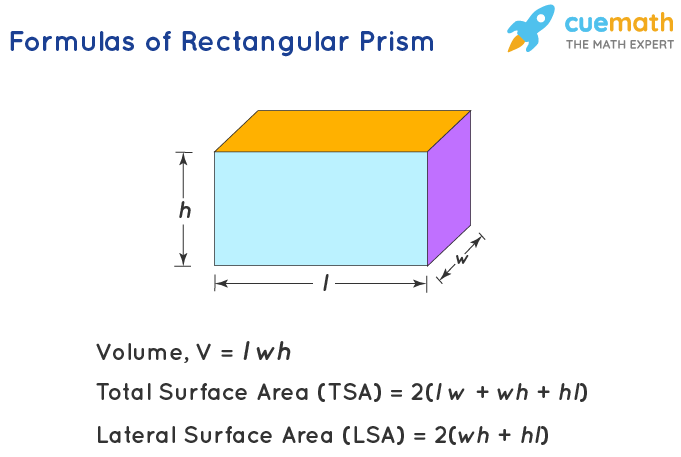
Let us see how to derive these formulas.
Volume of Rectangular Prism
The volume of a rectangular prism is the space that is inside it. We know that the volume of any prism is obtained by multiplying its base area by its height. Here,
- The base area of the rectangular prism = lw (using the area of a rectangle formula)
- The height of the rectangular prism = h
Thus, the volume of the rectangular prism, V = lw × h = lwh.
Surface Area of Rectangular Prism
There are two types of surface areas of a rectangular prism, one is the total surface area (TSA) and the other is the lateral surface area (LSA).
- The total surface area of a rectangular prism is the sum of the areas of all of its faces.
- The lateral surface area of a rectangular prism is the sum of the areas of all its side faces (excluding the bases).
We can calculate the areas of the side faces of a rectangular prism using its net.
The total surface area (TSA) of a rectangular prism
= The sum of areas of all faces
= lw + lw + wh + wh + hl + hl
= 2 (lw + wh + hl)
The lateral surface area (LSA) of a rectangular prism
= The sum of areas of side faces
= wh + wh + hl + hl
= 2 (wh + hl)
We will see the applications of these volume and surface area formulas of a rectangular prism in the section of Rectangular Prism Examples given below.
☛ Related Links
FAQs on Rectangular Prism
What is a Rectangular Prism?
A rectangular prism is a 3-d solid shape that has 6 rectangular faces in which all the pairs of opposite faces are congruent. It has 8 vertices, 6 faces, and 12 edges. A few real-life examples of a rectangular prism include rectangular fish tanks, shoe boxes, etc.
What is a Rectangular Prism also Known as?
A rectangular prism is also known as a cuboid. It resembles a cube, but it is not a cube. All its properties are the same as that of a cube except that its faces are rectangles, whereas the faces of a cube are squares.
What is the Difference Between a Cube and a Rectangular Prism (Cuboid)?
Both cube and cuboid are prisms. A cube has 6 faces which are identical squares whereas a rectangular prism has 6 faces in which all the faces are rectangles. The opposite faces in a rectangular prism are identical.
What is the Ratio of Corners to Faces in Rectangular Prisms?
A rectangular prism has 8 corners (vertices) and 6 faces. So the ratio of the corners to faces in a rectangular prism is 8 : 6 (or) 4 : 3.
Why is a Rectangular Prism Called a Polyhedron?
A polyhedron is a 3-d shape in which all the 6 faces are in the shape of a polygon, i.e., in a polyhedron, the top and bottom faces are congruent polygons and the remaining 4 faces are lateral faces that are parallelograms. Therefore, it is called a polyhedron.
What is the Volume of a Rectangular Prism?
The volume of a rectangular prism is the space inside the prism. It is calculated by multiplying its base area by its height. Thus, the formula for the volume of a rectangular prism is Volume (V) = lwh; where 'l' is the length, 'w' is the width, and 'h' is the height of the prism and its base area (area of the rectangle of length 'l' and width 'w') is lw.
What is the Total Surface Area of a Rectangular Prism?
The total surface area of a rectangular prism is obtained by adding the areas of all its faces. Thus, the total surface area (TSA) of a rectangular prism is TSA = 2 (lw + wh + hl); where 'l' is the length, 'w' is the width, and 'h' is the height of the prism.
What is the Lateral Surface Area of a Rectangular Prism?
The lateral surface area of a rectangular prism is the sum of the areas of all its faces excluding the bases. Thus, the lateral surface area (LSA) of a rectangular prism of length 'l', width 'w', and height 'h' is LSA = 2 (wh + hl).
What is the Net of a Rectangular Prism?
The net of a rectangular prism is a two-dimensional representation of the prism which shows the faces of the prism if they are laid out flat. The net of a triangular prism has 6 rectangles in which 2 rectangles are the bases and the other 4 rectangles are its lateral faces.
What is a Right Rectangular Prism?
A right rectangular prism is a three-dimensional (3D) solid shape which has 6 faces, 12 edges, and 8 vertices. It is commonly known as the cuboid. All the angles that are formed at the vertices of this prism are right angles.